早教吧作业答案频道 -->物理-->
如图所示,在第一象限有向下的匀强电场,在第四象限有垂直纸面向里的有界匀强磁场.在y轴上坐标为(0,b)的M点,质量为m,电荷量为q的正点电荷(不计重力),以垂直于y轴的初速度v0
题目详情
如图所示,在第一象限有向下的匀强电场,在第四象限有垂直纸面向里的有界匀强磁场.在y轴上坐标为(0,b)的M点,质量为m,电荷量为q的正点电荷(不计重力),以垂直于y轴的初速度v0水平向右进入匀强电场.恰好从x轴上坐标为(2b,0)的N点进入有界磁场.磁场位于y=-0.8b和x=4b和横轴x、纵轴y所包围的矩形区域内.最终粒子从磁场右边界离开.求:
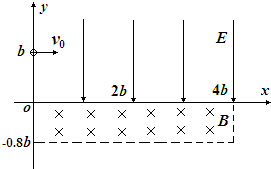
(1)匀强电场的场强大小E;
(2)磁感应强度B的最大值;
(3)磁感应强度B最小值时,粒子能否从(4b,-0.8b)处射出?画图说明.

(1)匀强电场的场强大小E;
(2)磁感应强度B的最大值;
(3)磁感应强度B最小值时,粒子能否从(4b,-0.8b)处射出?画图说明.
▼优质解答
答案和解析
(1)粒子在匀强电场中做类平抛运动:
竖直位移为 y=b=
at2;
水平位移为 x=2b=v0t;
其加速度 a=
可得电场强度 E=
(2)根据动能定理,设粒子进入磁场时的速度大小为v
有
mv2-
m
=qEb
代入E可得 v=
v0
v与正x轴的夹角θ有 cosθ=
=
所以θ=45°
粒子在匀强磁场中做匀速圆周运动,有 qvB=m
解得 B=
磁场越强,粒子运动的半径越小,从右边界射出的最小半径即从磁场右上角(4b,0)处射出,由几何关系得:
rmin=
=
b
可得 Bmax=
(3)不能.图画如下.
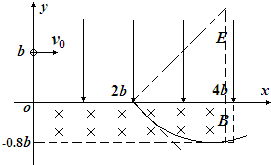
答:
(1)匀强电场的场强大小E为
;
(2)磁感应强度B的最大值为
;
(3)磁感应强度B最小值时,粒子不能从(4b,-0.8b)处射出.
竖直位移为 y=b=
| 1 |
| 2 |
水平位移为 x=2b=v0t;
其加速度 a=
| qE |
| m |
可得电场强度 E=
m
| ||
| 2qb |
(2)根据动能定理,设粒子进入磁场时的速度大小为v
有
| 1 |
| 2 |
| 1 |
| 2 |
| v | 2 0 |
代入E可得 v=
| 2 |
v与正x轴的夹角θ有 cosθ=
| v0 |
| v |
| ||
| 2 |
所以θ=45°
粒子在匀强磁场中做匀速圆周运动,有 qvB=m
| v2 |
| r |
解得 B=
| ||
| qr |
磁场越强,粒子运动的半径越小,从右边界射出的最小半径即从磁场右上角(4b,0)处射出,由几何关系得:
rmin=
| 4b-2b |
| 2sinθ |
| 2 |
可得 Bmax=
| mv0 |
| qb |
(3)不能.图画如下.

答:
(1)匀强电场的场强大小E为
m
| ||
| 2qb |
(2)磁感应强度B的最大值为
| mv0 |
| qb |
(3)磁感应强度B最小值时,粒子不能从(4b,-0.8b)处射出.
看了如图所示,在第一象限有向下的匀...的网友还看了以下:
在场强为E的匀强电场中,取O点为圆心,r为半径作一圆周,在O点固定一电荷量为+Q的点电荷,a、b、 2020-05-13 …
线圈匀速通过有界磁场,通过导体截面的电荷量线圈面积为S,感应强度为B,垂直于匀强磁场(大于线圈但用 2020-06-23 …
(2014•江苏二模)在半径为r、电阻为R的圆形导线框内,以直径为界,左、右两侧分别存在着方向如图 2020-07-12 …
空间存在相互垂直的匀强电场E和匀强磁场B,其方向如图所示.一带电粒子+q以初速度υ0垂直于电场和磁 2020-07-22 …
如图所示,在光滑的水平面上,有一垂直向下的匀强磁场分布在宽为L的区域内,有一个边长为a(a<L)的 2020-07-31 …
如图,在光滑水平面上,有一竖直向下的匀强磁场,分布在宽为a的区域内,现有一边长为L(a>L)的正方形 2020-11-11 …
电场中的几道小问题1.在场强为E的均匀电场中,有一半径为R,长为L的圆柱面,其轴线与E方向垂直,在通 2020-11-26 …
(2007•江苏模拟)在竖直平面内有一边长为l的正方形区域处在场强为E的匀强电场中,电场方向与正方形 2020-12-09 …
在竖直平面内有一边长为l的正方形区域处在场强为E的匀强电场中,电场方向与正方形一边平行.一质量为m、 2020-12-09 …
质子和α粒子垂直于场强方向从同一点飞入同一匀强电场,且均不能飞出.若它们初速度相同,则在场内飞行时间 2021-01-13 …