早教吧作业答案频道 -->数学-->
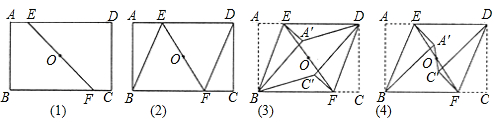
在学习完矩形的内容后,某课外学习小组对矩形的运动问题进行了研究,如图,在矩形ABCD中,AB=4,BC=6,点O为矩形ABCD对角线的交点.操作发现:如图(1)所示,点E为AD边上任意一点,连接E
题目详情
在学习完矩形的内容后,某课外学习小组对矩形的运动问题进行了研究,如图,在矩形ABCD中,AB=4,BC=6,点O为矩形ABCD对角线的交点.
操作发现:
如图(1)所示,点E为AD边上任意一点,连接EO并延长与BC边交于点F.
(1)小组成员甲发现“AE=CF”,请你完成证明;
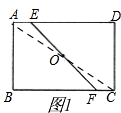
(2)如图(2),连接BE、DF,小组成员乙发现“四边形BEDF的形状一定是___,当AE的长为___时,四边形BEDF是菱形”;
探究发现:
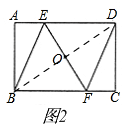
受前面两位组员的启发,小组成员丙与丁对图形进一步操作,将图(2)中的△ABE与△CDF分别沿BE与DF进行翻折,点A与点C分别落在矩形ABCD内的点A′,C′处.
(3)如图(3),连接A′D,BC′,发现“四边形BA′DC′是平行四边形”,请你证明这个结论;
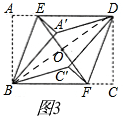
(4)如图(4),连接A′C′,A′C′有最小值吗?若有,请你直接写出AE的长;若没有,请说明理由.
操作发现:
如图(1)所示,点E为AD边上任意一点,连接EO并延长与BC边交于点F.
(1)小组成员甲发现“AE=CF”,请你完成证明;
(2)如图(2),连接BE、DF,小组成员乙发现“四边形BEDF的形状一定是___,当AE的长为___时,四边形BEDF是菱形”;
探究发现:
受前面两位组员的启发,小组成员丙与丁对图形进一步操作,将图(2)中的△ABE与△CDF分别沿BE与DF进行翻折,点A与点C分别落在矩形ABCD内的点A′,C′处.
(3)如图(3),连接A′D,BC′,发现“四边形BA′DC′是平行四边形”,请你证明这个结论;
(4)如图(4),连接A′C′,A′C′有最小值吗?若有,请你直接写出AE的长;若没有,请说明理由.

▼优质解答
答案和解析
(1)证明:如图1,连接AC,
∴点O在线段AC上,AD∥BC,OA=OC,
∴∠AOE=∠COF,∠EAO=∠FCO,
∴△AOE≌△COF,
∴AE=CF;
(2) 如图2,连接BD,
∵四边形ABCD为矩形,
∴AB=CD,∠BAE=∠DCF,
由(1)有AE=CF,
∴DE=BF
Rt△ABE≌Rt△CDF,
∴BE=DF,
∵EF=EF,
∴四边形BEDF是平行四边形.
设AE=x,则DE=6-x,
∵四边形BEDF是菱形,
∴BE=BD=6-x,
在Rt△ABE中,AB=4,
根据勾股定理,得 AB2+AE2=BE2,
∴16+x2=(6-x)2,
∴x=
.
故答案为平行四边形,
.
(3) 如图3,连接BD,由(1)有,AE=CF,
∵四边形ABCD为矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=CDF,
∵沿BE翻折,点A落在A′处,
∴Rt△ABE≌Rt△A′BE,
∴A′B=AB,∠ABE=∠A′BE=
∠ABA′
同理可得,C′D=CD,∠CDF=∠C′DF=
∠C′DC,
∴∠ABA′=∠C′DC,A′B=C′D,
∠ABO-∠ABA′=∠CDO-∠CDC′,
∴∠OBA′=∠ODC′,
∴A′B∥C′D,
∴四边形BA′DC′是平行四边形;
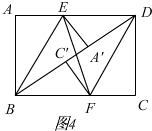
(4) 如图4,要使A′C′最小,只有点A′,C′落在矩形对角线BD上,
设AE=x,
∴EA′=x,DE=6-x,矩形的对角线BD=
=2
,
由对折有BA′=BA=4
∴DA′=BD-BA′=2
-4,
在Rt△DEA′中,有DE2=EA′2+DA′2,
∴(6-x)2=x2+(2
-4)2
∴x=
,
即:AE=
.

(1)证明:如图1,连接AC,
∴点O在线段AC上,AD∥BC,OA=OC,
∴∠AOE=∠COF,∠EAO=∠FCO,
∴△AOE≌△COF,
∴AE=CF;

(2) 如图2,连接BD,
∵四边形ABCD为矩形,
∴AB=CD,∠BAE=∠DCF,
由(1)有AE=CF,
∴DE=BF
Rt△ABE≌Rt△CDF,
∴BE=DF,
∵EF=EF,
∴四边形BEDF是平行四边形.
设AE=x,则DE=6-x,
∵四边形BEDF是菱形,
∴BE=BD=6-x,
在Rt△ABE中,AB=4,
根据勾股定理,得 AB2+AE2=BE2,
∴16+x2=(6-x)2,
∴x=
| 3 |
| 5 |
故答案为平行四边形,
| 3 |
| 5 |

(3) 如图3,连接BD,由(1)有,AE=CF,
∵四边形ABCD为矩形,
∴∠A=∠C=90°,AB=CD,AB∥CD,
∴Rt△ABE≌Rt△CDF,
∴∠ABE=CDF,
∵沿BE翻折,点A落在A′处,
∴Rt△ABE≌Rt△A′BE,
∴A′B=AB,∠ABE=∠A′BE=
| 1 |
| 2 |
同理可得,C′D=CD,∠CDF=∠C′DF=
| 1 |
| 2 |
∴∠ABA′=∠C′DC,A′B=C′D,
∠ABO-∠ABA′=∠CDO-∠CDC′,
∴∠OBA′=∠ODC′,
∴A′B∥C′D,
∴四边形BA′DC′是平行四边形;

(4) 如图4,要使A′C′最小,只有点A′,C′落在矩形对角线BD上,
设AE=x,
∴EA′=x,DE=6-x,矩形的对角线BD=
| BC2+CD2 |
| 13 |
由对折有BA′=BA=4
∴DA′=BD-BA′=2
| 13 |
在Rt△DEA′中,有DE2=EA′2+DA′2,
∴(6-x)2=x2+(2
| 13 |
∴x=
4
| ||
| 3 |
即:AE=
4
| ||
| 3 |
看了在学习完矩形的内容后,某课外学...的网友还看了以下:
根据每个细胞中DNA的相对含量不同,将某种连续增殖的动物细胞归为甲、乙、丙三组,每组细胞数如下图1 2020-05-17 …
以下关于如图的描述正确的是()A、图中锋面过境时,可能出现狂风暴雨的天气B、图中降水多发生在锋前, 2020-06-26 …
如图所示,BC为半径R=0.144m的14圆弧,AB为光滑水平轨道,两轨道在B处相切连接;AB轨道 2020-07-03 …
如图中的(a)图所示,一个500匝的线圈的两端跟R=99Ω的电阻相连,置于竖直向下的匀强磁场中,线 2020-07-05 …
关于多用电表的使用,下列操作(如图)正确的是()A.测电压时,应按如图连接方式测量B.测电流时,应 2020-07-16 …
A、B为两等量异种电荷,图中水平虚线为A、B连线的中垂线,现将另两个等量异种的检验电荷a、b,如图 2020-07-17 …
反比例函数y=kx(x>0)的图象如图,点A是图象上的点,连接OA并延长到B,使得BA=OA,BC 2020-07-20 …
下图为DNA分子的某一片段,其中①②③分别表示某种酶的作用部位,则相应的酶依次是[]A.DNA连接 2020-07-29 …
一本连环画.文字页和插图页的排列规律是文图图图文图图图…这本连环画共有96页且最后1页是插图.这本连 2020-12-12 …
按要求填空:(1)在A图中,稀硫酸为电解质溶液,用导线连接后,铜片电极反应式.(2)在B图中外接直流 2021-01-24 …