早教吧作业答案频道 -->数学-->
矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为点D′,直线D′E交AB边于点F,如果DE=x,D′F=y.(1)求y关于x的函数解析式及x的取值范围;(2)当点D的对应点D′
题目详情
矩形ABCD中,AD=5,AB=7,点E为DC上一个动点,把△ADE沿AE折叠,点D的对应点为点D′,直线D′E交AB边于点F,如果DE=x,D′F=y.
(1)求y关于x的函数解析式及x的取值范围;
(2)当点D的对应点D′落在∠ABC的角平分线上时,求此时DE的长.
(1)求y关于x的函数解析式及x的取值范围;
(2)当点D的对应点D′落在∠ABC的角平分线上时,求此时DE的长.
▼优质解答
答案和解析
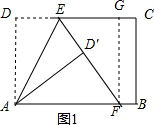 (1)如图1,过F作FG⊥CD于G,
(1)如图1,过F作FG⊥CD于G,
∴四边形BFGC是矩形,
∴FG=BC=AD=5,∠FGE=∠CGF=90°,
∵把△ADE沿AE折叠得到△AED′,
∴AD′AD=5,∠AD′E=ADE=90°,
∴∠AD′F=90°,
在△AD′F与△EFG中,
,
∴△AD′F≌△EFG,
∴AF=EF=x+y,GE=D′F=y,
∵GE2+FG2=EF2,
即y2+52=(x+y)2,
∴y=
,(0<x<7-2
);
(2)如图2,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P
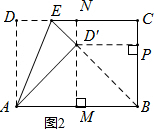 ∵点D的对应点D′落在∠ABC的角平分线上,
∵点D的对应点D′落在∠ABC的角平分线上,
∴MD′=PD′,
设MD′=x,则PD′=BM=x,
∴AM=AB-BM=7-x,
又折叠图形可得AD=AD′=5,
∴x2+(7-x)2=25,解得x=3或4,
即MD′=3或4.
在Rt△END′中,设ED′=a,
①当MD′=3时,AM=7-3=4,D′N=5-3=2,EN=4-a,
∴a2=22+(4-a)2,
解得a=
,即DE=
,
②当MD′=4时,AM=7-4=3,D′N=5-4=1,EN=3-a,
∴a2=12+(3-a)2,
解得a=
,即DE=
.
综上所述:DE=
或
.
 (1)如图1,过F作FG⊥CD于G,
(1)如图1,过F作FG⊥CD于G,∴四边形BFGC是矩形,
∴FG=BC=AD=5,∠FGE=∠CGF=90°,
∵把△ADE沿AE折叠得到△AED′,
∴AD′AD=5,∠AD′E=ADE=90°,
∴∠AD′F=90°,
在△AD′F与△EFG中,
|
∴△AD′F≌△EFG,
∴AF=EF=x+y,GE=D′F=y,
∵GE2+FG2=EF2,
即y2+52=(x+y)2,
∴y=
| 25-x2 |
| 2x |
| 6 |
(2)如图2,连接BD′,过D′作MN⊥AB,交AB于点M,CD于点N,作D′P⊥BC交BC于点P
 ∵点D的对应点D′落在∠ABC的角平分线上,
∵点D的对应点D′落在∠ABC的角平分线上,∴MD′=PD′,
设MD′=x,则PD′=BM=x,
∴AM=AB-BM=7-x,
又折叠图形可得AD=AD′=5,
∴x2+(7-x)2=25,解得x=3或4,
即MD′=3或4.
在Rt△END′中,设ED′=a,
①当MD′=3时,AM=7-3=4,D′N=5-3=2,EN=4-a,
∴a2=22+(4-a)2,
解得a=
| 5 |
| 2 |
| 5 |
| 2 |
②当MD′=4时,AM=7-4=3,D′N=5-4=1,EN=3-a,
∴a2=12+(3-a)2,
解得a=
| 5 |
| 3 |
| 5 |
| 3 |
综上所述:DE=
| 5 |
| 2 |
| 5 |
| 3 |
看了矩形ABCD中,AD=5,AB...的网友还看了以下:
点C在数轴上对应的点所对应数是0.5,点Q为数轴上B点右侧一动点,当点在数轴上移动式,求QA+QB 2020-05-13 …
如图,数轴上点A,B,D对应点的数分别是-400.200-800,动点P,Q分别从点D,O同时出发 2020-06-12 …
已知Z∈C,在复平面内,Z,对应的点分别为P、P2,O为坐标原点,则在下列结论中正确的为①当Z为纯 2020-06-14 …
学苑新报上的,已知点A在数轴上对应的数为a,点B在数轴上对应的数为b,且|a+4|+(b-1)²= 2020-07-15 …
求当实数m为何值时,z=[(m^2-m-6)/(m+3)]+(m^2+5m+6)i(1)为纯虚数( 2020-08-01 …
全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形.假设△ABC和△ 2020-08-01 …
如图,数轴上有A、B两点,分别对应的数为a、b,已知(a+1)的平方与|b-3|互为相反数,点P为数 2020-11-17 …
物理题某次军事演习中,进行汽车接应物资训练如图所示汽车停在A点待命接应地点为B物资在接应点B正上方的 2020-12-13 …
在数轴上,a、b、c所对应的点分别为A、B、C,点P为易动点,其对应的数为x.(a)当点P在AB间运 2020-12-17 …
辩论赛:家长应不应该适当的放开孩子?我是反方,应该适当的放开孩子.要有论据,论证,论点.要些事例.一 2020-12-30 …