早教吧作业答案频道 -->数学-->
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(
题目详情
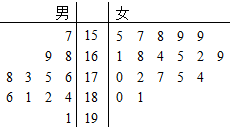
某小学对五年级的学生进行体质测试,已知五年一班共有学生30人,测试立定跳远的成绩用茎叶图表示如图(单位:cm):
男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.
(Ⅰ)求五年一班的女生立定跳远成绩的中位数;
(Ⅱ)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(Ⅲ)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
男生成绩在175cm以上(包括175cm)定义为“合格”,成绩在175cm以下(不包括175cm)定义为“不合格”.
女生成绩在165cm以上(包括165cm)定义为“合格”,成绩在165cm以下(不包括165cm)定义为“不合格”.

(Ⅰ)求五年一班的女生立定跳远成绩的中位数;
(Ⅱ)在五年一班的男生中任意选取3人,求至少有2人的成绩是合格的概率;
(Ⅲ)若从五年一班成绩“合格”的学生中选取2人参加复试,用X表示其中男生的人数,写出X的分布列,并求X的数学期望.
▼优质解答
答案和解析
(I)由茎叶图得五年一班的女生立定跳远成绩的中位数为
=166.5cm.…(2分)
(II)设“仅有两人的成绩合格”为事件A,“有三人的成绩合格”为事件B,
至少有两人的成绩是合格的概率:P=P(A)+P(B),
又男生共12人,其中有8人合格,从而P(A)=
,(4分)
P(B)=
,所以p=
.(6分)
(III)因为女生共有18人,其中有10人合格,
依题意,X的取值为0,1,2.
则P(X=0)=
=
,
P(X=1)=
=
,
P(X=2)=
=
,
(每项1分)(10分)
因此,X的分布列如下:
∴E(X)=0×
+1×
+2×
=
=
(人).(未化简不扣分)(12分)
(或是,因为X服从超几何分布,所以E(X)=2×
=
| 165+168 |
| 2 |
(II)设“仅有两人的成绩合格”为事件A,“有三人的成绩合格”为事件B,
至少有两人的成绩是合格的概率:P=P(A)+P(B),
又男生共12人,其中有8人合格,从而P(A)=
| ||||
C
|
P(B)=
| ||
C
|
| 42 |
| 55 |
(III)因为女生共有18人,其中有10人合格,
依题意,X的取值为0,1,2.
则P(X=0)=
| ||||
|
| 5 |
| 17 |
P(X=1)=
| ||||
|
| 80 |
| 153 |
P(X=2)=
| ||||
|
| 28 |
| 153 |
(每项1分)(10分)
因此,X的分布列如下:
| X | 0 | 1 | 2 | ||||||
| P |
|
|
|
| 5 |
| 17 |
| 80 |
| 153 |
| 28 |
| 153 |
| 136 |
| 153 |
| 8 |
| 9 |
(或是,因为X服从超几何分布,所以E(X)=2×
| 8 |
| 18 |
看了某小学对五年级的学生进行体质测...的网友还看了以下:
全班有62人,其中有5分之1男生和8名女生去参加婚礼,剩下男女生相等.全班男女生各有多少人?...全 2020-03-30 …
在下列事实所伴随的变化中,肯定属于化学变化的有1分子种类发生变化2分子间的间隔发生改变3有发光、发 2020-04-26 …
某校七年级两个班的115名同学积极参加,已知 甲班1/3的学生每人捐款10元,乙班2/5同学捐10 2020-05-16 …
快、、、、、、、初一两个班的115名学生参加捐款,已知甲班1/3的学生每人捐款10元,乙班2/5的 2020-05-16 …
某校七年级两个班的115名同学积极参加,已知甲班1/3的学生每人捐款10元,乙班2/5同学捐10元 2020-05-16 …
某校5(1)班与5(2)班人数相等,其中五(1)班男生人数比五二班女生少20%,五二班男生人数与五 2020-05-20 …
某班原来女生占全班人数的5分之2.后来陆续转来了4名女生,这样女生占这时全班人数的11分之5,这个 2020-06-13 …
某中学有初一学生153某中学有初一学生153人,分成甲、乙、丙三班,乙班比丙班多5人而比甲班少8人 2020-07-18 …
5.某班男女生人数比是9:11,后来又转来2名男生.这时候男生人数占全班的10/21.原来这个班男女 2020-11-05 …
某班书画兴趣小组有4名男生,5名女生:求⑴从中选派5名学生参加一次活动,要求有女生某班书画兴趣小组有 2020-11-30 …
 扫描下载二维码
扫描下载二维码
