早教吧作业答案频道 -->数学-->
已知数列{an}中，a1=1，a2=a-1（a≠0且a≠1），其前n项和为Sn，且当n≥2时，．（Ⅰ）求证：数列{Sn}是等比数列；（Ⅱ）求数列{an}的通项公式；（Ⅲ）若a=4，令，记数列{bn}的
题目详情
已知数列{a n }中，a 1 =1，a 2 =a-1（a≠0且a≠1），其前n项和为S n ，且当n≥2时，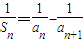
．
（Ⅰ）求证：数列{S n }是等比数列；
（Ⅱ）求数列{a n }的通项公式；
（Ⅲ）若a=4，令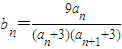
，记数列{b n }的前n项和为T n ．设λ是整数，问是否存在正整数n，使等式
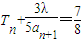成立？若存在，求出n和相应的λ值；若不存在，请说明理由．
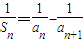．（Ⅰ）求证：数列{S n }是等比数列；
（Ⅱ）求数列{a n }的通项公式；
（Ⅲ）若a=4，令
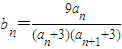，记数列{b n }的前n项和为T n ．设λ是整数，问是否存在正整数n，使等式 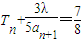成立？若存在，求出n和相应的λ值；若不存在，请说明理由．▼优质解答
答案和解析
分析：（Ⅰ）由an=sn-sn-1得：=-化简得Sn2=Sn-1Sn+1（n≥2）得到数列{Sn}是等比数列；（Ⅱ）由（1）得等比数列{Sn}的首项为1，公比为a，求出sn，利用an=sn-sn-1得到即可；（Ⅲ）根据a=4，令，化简得到bn的通...
看了 已知数列{an}中，a1=1...的网友还看了以下：
读下面这段文字，根据拼音写出汉字。江南的冬景，不（jīn）令人感叹不已。记得儿时大雪纷飞，记起雪天 2020-05-13 …
对于正项数列{an},记Hn=/(a1+a2/2 +a3/3 +----+an/n ),若Hn=1 2020-05-16 …
在1与2之间插入n个正数a1,a2,a3,…,an,使这n+2个数成等比数列；又在1与2间插入n个 2020-05-16 …
a1=2,an=2-1/an-1(n≥2),令bn=1/an-1已知数列{an}满足a1=2,an 2020-06-17 …
已知数列an中,a1=3,a2=5,其前n项和Sn满足Sn+Sn-2=2Sn-1+2^n-1(n> 2020-07-16 …
已知数列{a下标n}（后都为下标）满足：a1=4an=4-4/a(n-1)此处括号内位下标(n≥2 2020-07-29 …
1.设{an}是公比为q的等比数列,|q|>1,令bn=an+1(n=1,2,…),若数列{bn} 2020-08-01 …
设数列{an}是一个无穷数列，记Tn＝n+2i＝12i−1ai+2a1−a3−2n+2an+1，n 2020-08-02 …
（2011•镇江一模）设数列{an}是一个无穷数列，记Tn＝n+2i＝12i−1ai+2a1−a3− 2020-11-12 …
已知直线y=[-(n+1)/(n+2)]x+[1/(n+2)](n为正整数)与两坐标轴围成的三角形面 2021-02-03 …