早教吧作业答案频道 -->数学-->
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,(1)求证:四边形MENA是平行四边形;(2)求∠BPM的度数.
题目详情
如图,在△ABC中,∠C=90°,AM与BN交于点P,且BM=AC,AN=CM,△EMC是等腰直角三角形,
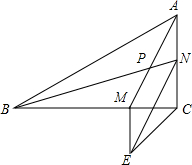
(1)求证:四边形MENA是平行四边形;
(2)求∠BPM的度数.

(1)求证:四边形MENA是平行四边形;
(2)求∠BPM的度数.
▼优质解答
答案和解析
(1)证明:∵△EMC是等腰直角三角形,
∴MC=ME,∠CME=90°,
∵∠C=90°,
∴AC∥ME,
∵AN=CM,
∴AN=ME,
∴四边形MENA是平行四边形;
(2) 连接BE,
∵四边形AMEN为平行四边形,
∴NE=AM,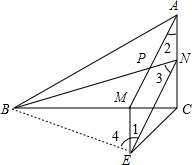 ∠2=∠1,AM∥EN,
∠2=∠1,AM∥EN,
∴∠3=∠BPM,
在△BEM和△AMC中,
,
∴△BEM≌△AMC(SAS),
∴∠4=∠AMC,BE=AM,
∵∠2+∠AMC=90°,
∴∠1+∠4=90°,
∵NE=AM,BE=AM,
∴△BEN为等腰直角三角形,∠BNE=45°,
∴∠BPM=∠3=45°.
∴MC=ME,∠CME=90°,
∵∠C=90°,
∴AC∥ME,
∵AN=CM,
∴AN=ME,
∴四边形MENA是平行四边形;
(2) 连接BE,
∵四边形AMEN为平行四边形,
∴NE=AM,
 ∠2=∠1,AM∥EN,
∠2=∠1,AM∥EN,∴∠3=∠BPM,
在△BEM和△AMC中,
|
∴△BEM≌△AMC(SAS),
∴∠4=∠AMC,BE=AM,
∵∠2+∠AMC=90°,
∴∠1+∠4=90°,
∵NE=AM,BE=AM,
∴△BEN为等腰直角三角形,∠BNE=45°,
∴∠BPM=∠3=45°.
看了 如图,在△ABC中,∠C=9...的网友还看了以下:
四项因式分解的题.a^2-ab+ac-bc,x^2+ax^2+x+ax-1-a,ac^2+bd^2 2020-05-13 …
化简计算(式中a,b,c两两不相等)?(a^2-ab-ac+bc分之2a-b-c)+(b^2-ab 2020-05-23 …
2)已知:a/(bc-a^2)+b/(ac-b^2)+c/(ab-c^2)=0求证:a/(bc-a 2020-07-25 …
1.已知二次三项式21x^2+ax-10可分解为两个整系数的一次因式之级,那么a是奇数?偶数?负数 2020-07-31 …
数学归纳法的题用数学归纳法证明1+a+a^2+a^3+.+a^(n+1)=[1-a^(n+2)]/ 2020-08-01 …
二次根式的运算(请给出过程)已知a+b+c=abc0,试求代数式(1-b^2)(1-c^2)/(b 2020-08-02 …
高一数学,紧急!1.已知三角形ABC中,a=3,b=6,c=60度,则向量BC乘向量CA=2.已知 2020-08-02 …
1、a^2+ab+ac+bc2、ax-2bx+ay-2by3、x^3+3x^2-4x-124、ab- 2020-12-29 …
已知直线Y=MX-1与反比例函数Y=K/X的图像交于AB两点A(2.1)在x轴上是否存在点c使|BC 2021-01-10 …
初中数学,因式分解!1.-28m^2-3m^3+m^42.a^n+1-5a^n+6a^n-13.(2 2021-01-22 …