早教吧作业答案频道 -->数学-->
如图,已知四边形ABCD是O的内接四边形,过点A的切线与CB的延长线交于点P,且PA=82,PB=8.(1)若∠APB=45°求∠D的大小;(2)若O的半径为5,求圆心O到直线BC的距离.
题目详情
如图,已知四边形ABCD是 O的内接四边形,过点A的切线与CB的延长线交于点P,且PA=8
,PB=8.
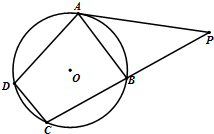
(1)若∠APB=45°求∠D的大小;
(2)若 O的半径为5,求圆心O到直线BC的距离.
| 2 |

(1)若∠APB=45°求∠D的大小;
(2)若 O的半径为5,求圆心O到直线BC的距离.
▼优质解答
答案和解析
(1)在△PAB中,有PA=8
,PB=8,∠APB=45°.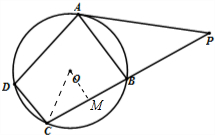
由余弦定理得:AB2=82+(8
)2-2×8×8
cos45°=64,解得AB=8.
∴AB=PB,∠BAP=45°,
∴∠ABP=Rt∠.
所以△PAB为Rt△,即AB⊥PC.
所以∠ABC=90°,
又因为四边形ABCD是 O的内接四边形,
所以∠D=90°.
(2)连接OC,作OM⊥BC于M,
由垂径定理可知:M为BC的中点,
由切割线定理得:PA2=PB•PC,
又PA=8
,PB=8,
所以PC=16,BC=8,MC=4.
因为 O的半径为5,所以在Rt△OMT中有,OM=3,
所求圆心O到直线BC的距离为3.
| 2 |

由余弦定理得:AB2=82+(8
| 2 |
| 2 |
∴AB=PB,∠BAP=45°,
∴∠ABP=Rt∠.
所以△PAB为Rt△,即AB⊥PC.
所以∠ABC=90°,
又因为四边形ABCD是 O的内接四边形,
所以∠D=90°.
(2)连接OC,作OM⊥BC于M,
由垂径定理可知:M为BC的中点,
由切割线定理得:PA2=PB•PC,
又PA=8
| 2 |
所以PC=16,BC=8,MC=4.
因为 O的半径为5,所以在Rt△OMT中有,OM=3,
所求圆心O到直线BC的距离为3.
看了 如图,已知四边形ABCD是O...的网友还看了以下:
a,b,c且a<b<c,试找出它们的共同点,并证明你的结论.a=3,b=4,c=5(3^2+4^2= 2020-03-30 …
已知实数a、b、c满足a2+ b 2=1,b 2+ c2=2,c2+ a2=2,则ab+bc+ca 2020-04-05 …
下列语句写成数学式子正确的是()A.9是81的算术平方根:±81=9B.5是(-5)2的算术平方根 2020-04-11 …
六年级英语题一、选出划线部分读音不同的单词。(5分)()(1)A.babyB.takeC.dayD 2020-05-14 …
设椭圆C1的离心率为5/13,焦点在x轴上且长轴长为26.若曲线C2上的点到椭圆C1的两个焦点的距 2020-05-15 …
与0.75÷25的结果相等的算式是()A.75÷0.25B.7.5÷250C.7.5÷2.5D.7 2020-07-13 …
定义运算:a⊙b=3a+5ab+kb,其中a,b为任意两个数,k为常数.比如:2⊙7=3×2+5× 2020-07-17 …
(1)二级等差数列:2,3,5,8,()A.8B.9C.15D.12(2)等差数列变式:3,4,6 2020-07-23 …
某几何体的直观图如图所示,则该几何体的侧(左)视图的面积为()A.5πa2B.5a2C.(5+2) 2020-08-01 …
(2011•大同一模)某几何体的直观图如图所示,则该几何体的侧(左)视图的面积为()A.5πa2B 2020-08-01 …