早教吧作业答案频道 -->数学-->
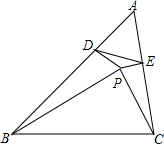
如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.
题目详情
如图,在△ABC中内取一点,使∠PBA=∠PCA,作PD⊥AB于点D,PE⊥AC于点E,求证:DE的垂直平分线必过BC的中点M.

▼优质解答
答案和解析
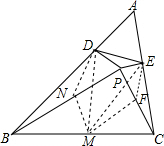 取BC,PB,PC的中点M,N,F,连接MN,MF,E,DN,DM,EM,
取BC,PB,PC的中点M,N,F,连接MN,MF,E,DN,DM,EM,
∴MF=
BP,MN=
PC,MF∥PN,MN∥PF,
∴四边形NMFP是平行四边形,
∴∠PNM=∠PFM,
∵PD⊥AB,PE⊥AC,
∴DN=
PB,EF=
PC,
∴DN=MF,MN=EF,
∵∠DNP=2∠ABP,∠PFE=2∠ACD,
∵∠ABP=∠ACD,
∴∠DNP=∠PFE,
∴∠DNM=∠EFM,
在△DNM与△MFE中,
,
∴△DNM≌△MFE,
∴DM=EM,
∴△DME是等腰三角形,
∴底边DE的垂直平分线(过M点)必是BC的中点M.
 取BC,PB,PC的中点M,N,F,连接MN,MF,E,DN,DM,EM,
取BC,PB,PC的中点M,N,F,连接MN,MF,E,DN,DM,EM,∴MF=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形NMFP是平行四边形,
∴∠PNM=∠PFM,
∵PD⊥AB,PE⊥AC,
∴DN=
| 1 |
| 2 |
| 1 |
| 2 |
∴DN=MF,MN=EF,
∵∠DNP=2∠ABP,∠PFE=2∠ACD,
∵∠ABP=∠ACD,
∴∠DNP=∠PFE,
∴∠DNM=∠EFM,
在△DNM与△MFE中,
|
∴△DNM≌△MFE,
∴DM=EM,
∴△DME是等腰三角形,
∴底边DE的垂直平分线(过M点)必是BC的中点M.
看了 如图,在△ABC中内取一点,...的网友还看了以下:
在等边三角形ABC中,D为线段BC上的动点,连接AD,在角ADC内作角ADE等于60度,交AC边于 2020-05-13 …
在等边三角形ABC中,D为线段BC上的动点,连接AD,在角ADC内作角ADE等于60度,交AC边于 2020-05-13 …
大学物理恒稳磁场无限长线圈B=unI中为什么n=1/d,期中d为线圈直径, 2020-06-14 …
下列关于无脊椎动物的叙述中正确的是()A.腔肠动物都可以食用B.扁形动物都是寄生虫C.环节动物都生 2020-06-18 …
水果中含有酸、甜或苦涩味道,决定这些味道的物质存在于细胞的()A.、叶绿体中B.细胞核中C.、液泡 2020-06-29 …
如图中四条曲线反映了我国1840~1956年四种经济成分的发展变化情况,其中D曲线代表的是何种经济 2020-07-13 …
大肠杆菌的遗传物质位于()A.拟核和质粒中B.线粒体和质粒中C.线粒体和叶绿体中D.线粒体和核糖体 2020-07-29 …
(2009•潮州二模)如图是线粒体内膜的结构示意图,其中F0和F1两部分构成了ATP合成酶.F0镶嵌 2020-11-12 …
下列关于无脊椎动物的叙述中正确的是()A、腔肠动物都可以食用B、扁形动物都是寄生虫C、环节动物都生活 2020-12-25 …
读人类文明进程及社会经济增长主导因素变化示意图,完成以下1~2题。图中d曲线表示的主导因素是A.土地 2021-01-13 …