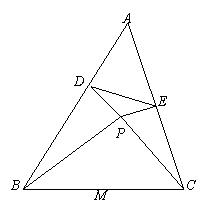
如图，在△ABC内取一点P，使∠PBA＝∠PCA，作PD⊥AB于D，PE⊥AC于E，求证：DE的垂直平分线必经过BC的中点M.

Question

如图，在 △ ABC 内取一点 P ，使 ∠ PBA ＝ ∠ PCA ，作 PD ⊥ AB 于 D ， PE ⊥ AC 于 E ，求证： DE 的垂直平分线必经过 BC 的中点 M .

Answer 1

解析： 如图，设 L 、 N 分别是 PB 、 PC 的中点，
连结 MD ， ME ， ML ， MN ， DL 和 EN
则 ML ∥ PC ，且 ML ＝ PC ； MN ∥ PB ，且 MN ＝ PB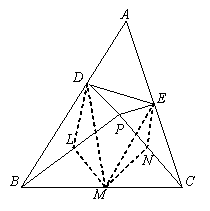
又由 ∠ PDB ＝ ∠ PEC ＝ 90° 知 DL ＝ PB ， EN ＝ PC
因此 DL ＝ MN     ①      ML ＝ EN     ②
并且 PLMN 为平行四边形        ……10 分
于是 ∠ PLM ＝ ∠ PNM
∠ DLP ＝ 2∠ PBA ＝ 2∠ PCA ＝ ∠ ENP
故 ∠ DLM ＝ ∠ DLP ＋ ∠ PLM ＝ ∠ ENP ＋ ∠ PNM ＝ ∠ ENM     ③
因而由 ①②③ 知 △ DML ≌△ MEN
故 DM ＝ EM ，从而 BC 的中点 M 在 DE 的垂直平分线上
即 DE 的垂直平分线必经过 BC 的中点 M .        ……20 分