距离是几何中的基本度量,几何问题和一些实际问题经常涉及距离,如建筑设计中常常需要计算空间两点间的距离.你能用两点的坐标表示这两点间的距离吗?
(1)在平面直角坐标系中 已知P 1 (x 1 y 1 ) P 2 (x 2 y 2 ) 则|P 1 P 2 |= ![]() .
.
(2)在空间直角坐标系 如图 设P 1 (x 1 y 1 z 1 ) P 2 (x 2 y 2 z 2 )是空间中任意两点 且点P 1 (x 1 y 1 z 1 ) P 2 (x 2 y 2 z 2 )在xOy平面上的射影分别为M、N 那么M、N的坐标为M(x 1 y 1 0)、N(x 2 y 2 0) 在xOy平面上 |MN|= ![]() .
.
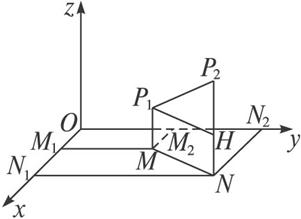
过点P 1 作P 2 N的垂线 垂足为H 则|MP 1 |=|z 1 | |NP 2 |=|z 2 | 所以|HP 2 |=|z 2 -z 1 |.
在Rt△P 1 HP 2 中 |P 1 H|=|MN|= ![]()
根据勾股定理 得
|P 1 P 2 |= ![]() =
= ![]() .
.
因此 空间中点P 1 (x 1 y 1 z 1 ) P 2 (x 2 y 2 z 2 )之间的距离
|P 1 P 2 |= ![]() .
.
(3)我们来确定P 1 、P 2 两点在柱坐标系中的距离公式:
根据空间点P的直角坐标(x y z)与柱坐标(ρ θ z)之间的变换公式: 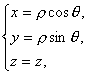 P 1 (x 1 y 1 z 1 ) P 2 (x 2 y 2 z 2 ) 有
P 1 (x 1 y 1 z 1 ) P 2 (x 2 y 2 z 2 ) 有 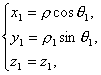 可得
可得 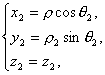
|P 1 P 2 |= ![]() .
.
(4)我们来确定P 1 、P 2 两点在球坐标系中的距离公式:
空间点P的直角坐标(x y z)与球坐标(r φ θ)之间的变换关系为 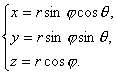
P 1 (x 1 y 1 z 1 ) P 2 (x 2 y 2 z 2 ) 有 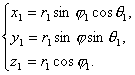 及
及 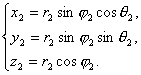 .
.
可得|P 1 P 2 |= ![]()
一辆卡车从A城开往B城,行驶了全程的三分之一,离中点还有20千米,问A、B两城相距多少千米? 2020-04-27 …
龙山乡挖一条水渠,现在已完成全长的三分之一,离中点还有五千米.这条水渠长多少米? 2020-04-27 …
鹿亭乡新建一条公路,现在己完成全长的三分之一,离中点还有五点五千米;.这条公路长多少米?(不要用方 2020-04-27 …
钟表怎样看时间?例:时针指向3和4中间,分针指向6,表示3点30分.问:钟面上表示的这个3点30是 2020-05-14 …
筑路队筑一条公路前两天修住了全长的四分之一离终点还有四十千米这条公路全长多少 2020-05-21 …
挖一条水渠,现在已经完成全长的三分之一离中点还有二分之一千米,这条水渠有多少千米? 2020-05-21 …
一辆汽车从甲地开往乙地,两小时行了全程的三分之一,离中点还有30千米,甲乙相距多少?有一堆煤,上午 2020-06-02 …
一条水渠修了全长的四分之一,离中点还有80米,这条水渠全长多少米? 2020-06-03 …
阅读以下年代标尺,回答问题。(1)在时间点A,中国发生了什么大事?(2)北京在时间点B遭遇了哪场浩 2020-07-08 …
英语中有过去将来时,为什么没有将来过去式,如果我想说将来的过去,该如何说过去将来时表示过去某一时间 2020-07-10 …