如图，多面体ABCDEF中，四边形ABCD是边长为2a的正方形，平面ADEF垂直于平面ABCD，且FA⊥AD，EF∥AD，EF=AF=a．（1）求证：BD⊥CF；（2）若P、Q分别为棱BF和DE的中点，求证：PQ∥平面ABCD；（3

Question

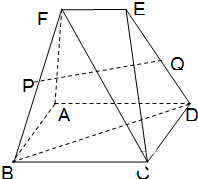如图，多面体ABCDEF中，四边形ABCD是边长为2a的正方形，平面ADEF垂直于平面ABCD，且FA⊥AD，EF∥AD，EF=AF=a．
（1）求证：BD⊥CF；
（2）若P、Q分别为棱BF和DE的中点，求证：PQ∥平面ABCD；
（3）求多面体ABCDEF的体积．

Answer 1

考点：
棱柱、棱锥、棱台的体积 空间中直线与直线之间的位置关系 直线与平面平行的判定
专题：
空间位置关系与距离
分析：
（1）连结AC，由已知得BD⊥AC，FA⊥平面ABCD，BD⊥AF，由此能证明BD⊥CF．（2）作PS⊥AB，QT⊥AD，EM⊥AD，S，T，M是垂足，由已知得四边形PSTQ是平行四边形，由此能证明PQ∥平面ABCD．（3）多面体ABCDEF的体积V=V四棱锥P-ABCD+V三棱锥C-DEF，由此能求出结果．

（1）证明：连结AC，∵ABCD是正方形，∴BD⊥AC，∵平面ABCD⊥平面ADEF，AF⊥AD，AD是两平面的交线，∴FA⊥平面ABCD，而BD?平面ABCD，∴BD⊥AF，又∵AC∩FA=A，∴BD⊥平面AFC，而CF?平在AFC，∴BD⊥CF．（2）证明：作PS⊥AB，QT⊥AD，EM⊥AD，S，T，M是垂足，在△ABF中，PS：AF=BP：BF=1：2，PS=12AF，在直角梯形中ADEF中，QT=12EM=12AF，∴PF∥.QT，∴四边形PSTQ是平行四边形，∴PQ∥ST，∴四边形PSTQ是平行四边形，∴PQ∥ST，而ST?平面ABCD，∴PQ∥平面ABCD．（3）多面体ABCDEF的体积：V=V四棱锥P-ABCD+V三棱锥C-DEF=13×(2a)2×a+13×12×a2×2a=53a2．
点评：
本题考查异面直线垂直的证明，考查直线与平面平行的证明，考查多面体的体积的求法，解题时要注意空间思维能力的培养．