如图，抛物线y=-x2+6x与x轴交于O，A两点，与直线y=2x交于O，B两点．点P在线段OA上以每秒1个单位的速度从点O向终点A运动，作EP⊥x轴交直线OB于E；同时在线段OA上有另一个动点Q，以每秒1个单位

Question

如图，抛物线y=-x²+6x与x轴交于O，A两点，与直线y=2x交于O，B两点．点P在线段OA上以每秒1个单位的速度从点O向终点A运动，作EP⊥x轴交直线OB于E；同时在线段OA上有另一个动点Q，以每秒1个单位的速度从点A向点O运动（不与点O重合）．作CQ⊥x轴交抛物线于点C，以线段CQ为斜边作如图所示的等腰直角△CQD．设运动时间为t秒．

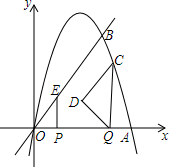
（1）求点B的坐标；
（2）当t=1秒时，求CQ的长；
（3）求t为何值时，点E恰好落在△CQD的某一边所在的直线上．

Answer 1

（1）∵抛物线y=-x²+6x与与直线y=2x交于O，B两点，
∴2x=-x²+6x，解得：x=0（舍去），x=4，
当x=4时，y=2×4=8．
故点B的坐标为（4，8）．
（2）∵抛物线y=-x²+6x与x轴交于O，A两点，
∴-x²+6x=0，解得：x=0（舍去），x=6，
即点A的坐标为（6，0）．
当t=1时，点C横坐标x=6-1=5，
点C纵坐标y=-5²+5×6=5．
故点C坐标为（5，5），
即当t=1秒时，CQ的长为5．
（3）过点D作DF⊥CQ于点F，如图所示．

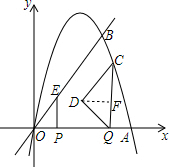
当时间为t时，E点坐标为（t，2t），C点坐标为（6-t，6t-t²）．
∵△CQD为等腰直角三角形，且CQ⊥x轴，
∴DF∥x轴，且∠CDF=∠QDF=45°，
∴Q点坐标为（6-t，0），
设CD所在的直线解析式为y=x+b₁，DQ所在的直线解析式为y=-x+b₂．
结合C、Q点的坐标可知：

6t-t2=6-t+b1

0=t-6+b2

，
解得：

b1=-t2+7t-6

b2=6-t

．
故CD所在直线的解析式为y=x-t²+7t-6，DQ所在的直线解析式为y=-x-t+6，
而CQ所在直线的解析式为x=6-t．
当点E在CD所在的直线上时，有2t=t-t²+7t-6，
解得：t=3±√(3)；
当点E在DQ所在的直线上时，有2t=-t-t+6，
解得：t=1.5；
当点E在CQ所在的直线上时，有t=6-t，
解得：t=3．
综上可知：当t=1.5或3-√(3)或3或3+√(3)时，点E恰好落在△CQD的某一边所在的直线上．