早教吧作业答案频道 -->数学-->
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为.
题目详情
在四面体A-BCD中,AB=BC=CD=AD,∠BAD=∠BCD=90°,二面角A-BD-C为直二面角,E是CD的中点,则∠AED的度数为___.

▼优质解答
答案和解析
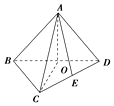
如图,设AB=BC=CD=AD=a,取BD的中点O,连接AO,CO,
则由题意可得AO⊥BD,CO⊥BD,AO=CO=
a,
∴∠AOC是二面角A-BD-C的平面角,
∵二面角A-BD-C为直二面角,∴∠AOC=90°.
在Rt△AOC中,由题意知AC=
=a,
∴△ACD为正三角形,
又∵E是CD的中点,
∴AE⊥CD,∴∠AED=90°.
故答案为:90°.

则由题意可得AO⊥BD,CO⊥BD,AO=CO=
| ||
| 2 |
∴∠AOC是二面角A-BD-C的平面角,
∵二面角A-BD-C为直二面角,∴∠AOC=90°.
在Rt△AOC中,由题意知AC=
| AO2+CO2 |
∴△ACD为正三角形,
又∵E是CD的中点,
∴AE⊥CD,∴∠AED=90°.
故答案为:90°.
看了 在四面体A-BCD中,AB=...的网友还看了以下:
O、A、B、C为空间四个点,又OA、OB、OC为空间的一个基底,则()A.O、A、B、C四点不共线 2020-05-14 …
平面内有三点ABC,其中ABC三点不共线,再找一点D,使得四边形ABCD为平行四边形,则满足条件的 2020-05-16 …
初四语文文言文下列句中,“则”的用法不同于其他一项的是()A.口耳之间则四寸耳B.处江湖之远则忧其 2020-05-16 …
促进个人与他人和谐要坚持四个原则,其中作为保证的是A诚信原则B平等原则C宽容原则D互促进个人与他人 2020-06-29 …
下列数阵是由偶数排列成的:(1)图中框内的四个数分别为a、b、c、d,则这四个数有什么关系(用式子 2020-07-18 …
下列说法中,正确的是()A.若非零向量AB与CD是共线向量,则A、B、C、D四点共线B.若a平行b 2020-08-01 …
(1)若a:c=d:b,则d叫做第比例项(2)若x:y=y:x,则y是x和z的.(3)6是3和的比 2020-08-02 …
ABCD四个人要派两个人出差分派时需要满足三个条件1若A去则C和D中要去一个人2B和C不能都去3C去 2020-10-31 …
A、B、C、D四名打字员承担一项打字任务,若由这四人中的某一人单独完成打字任务,则A需要24小时.B 2020-11-07 …
若四个数A/B/C/D,满足A+1=B-2=C+3=D-4,则A/B/C/D这四个数中最大的是()若 2020-11-19 …