早教吧作业答案频道 -->数学-->
三角形ABC中，AD是角平分线，AD的中垂线EF交BC的延长线于F，求证：FD是FB和FC的比例中项．
题目详情
三角形ABC中，AD是角平分线，AD的中垂线EF交BC的延长线于F，求证：FD是FB和FC的比例中项．
▼优质解答
答案和解析
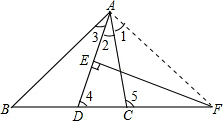证明：连结AF，如图所示：
∵AD的垂直平分线交AD于E，
∴AF=FD，
∴∠1+∠2=∠4，
∵∠B+∠3=∠4，
∠2=∠3，
∴∠B=∠1，
∵∠AFB=∠CFA，
∴△ACF∽△BAF，
∴
=
，
∴AF2=FB•FC，
即FD2=FB•FC；
即FD是FB和FC的比例中项．
证明：连结AF，如图所示：∵AD的垂直平分线交AD于E，
∴AF=FD，
∴∠1+∠2=∠4，
∵∠B+∠3=∠4，
∠2=∠3，
∴∠B=∠1，
∵∠AFB=∠CFA，
∴△ACF∽△BAF，
∴
| AF |
| FB |
| FC |
| AF |
∴AF2=FB•FC，
即FD2=FB•FC；
即FD是FB和FC的比例中项．
看了 三角形ABC中，AD是角平分...的网友还看了以下：
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料：AB与F作案；BD与A作案；CB与E 2020-05-16 …
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料:某刑事案件的六个嫌疑分子A,B,C, 2020-05-16 …
（2012•崇明县一模）已知：如图，在△ABC中，∠ACB=90°，AC=CB，CD⊥AB于D点， 2020-05-17 …
如图，△ABC的高AD为3，BC为4，直线EF∥BC，交线段AB于E，交线段AC于F，交AD于G， 2020-05-22 …
关于java的swap比如有[a,b,c,d,e]5个字母...用swap交换为[d,e,c,a, 2020-07-17 …
己知：如图1．正方形ABCD，过点A作∠EAF=90°，两边分别交直线BC于点E，交线段CD于点F 2020-07-17 …
如图，在射线BA、BC、AD、CD围成的菱形ABCD中，∠ABC=60°，AB=63，O是射线BD 2020-07-25 …
某刑事案件的六个嫌疑分子A,B,C,D,E,F交待了以下材料:某刑事案件的六个嫌疑分子A,B,C, 2020-07-29 …
如图所示,D,E,F是线段AB的四等分点.过点D作DH∥BC交AC于点H,过点E作EG∥BC交AC 2020-08-02 …
等腰三角形底角三等分交底边中线证角相等在等腰三角形ABC中,D是底边BC的中点,E,F是线段AD上 2020-08-02 …