顺次连接等腰梯形各边中点所得的四边形的形状是（）A.等腰梯形B.平行四边形C.矩形D.菱形

Question

顺次连接等腰梯形各边中点所得的四边形的形状是（　　）

A. 等腰梯形

B. 平行四边形

C. 矩形

D. 菱形

Answer 1

顺次连接等腰梯形各边中点所得的四边形是菱形，理由为：
已知：等腰梯形ABCD，E、F、G、H分别为AD、AB、BC、CD的中点，
求证：四边形EFGH为菱形．
证明：连接AC，BD，
∵四边形ABCD为等腰梯形，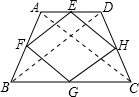
∴AC=BD，
∵E、H分别为AD、CD的中点，
∴EH为△ADC的中位线，
∴EH=(1)/(2)AC，EH∥AC，
同理FG=(1)/(2)AC，FG∥AC，
∴EH=FG，EH∥FG，
∴四边形EFGH为平行四边形，
同理EF为△ABD的中位线，
∴EF=(1)/(2)BD，又EH=(1)/(2)AC，且BD=AC，
∴EF=EH，
则四边形EFGH为菱形．
故选：D．