早教吧作业答案频道 -->数学-->
设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.(1)阅读填空如图①,已
题目详情
设ω是一个平面图形,如果用直尺和圆规经过有限步作图(简称尺规作图),画出一个正方形与ω的面积相等(简称等积),那么这样的等积转化称为ω的“化方”.
(1)阅读填空
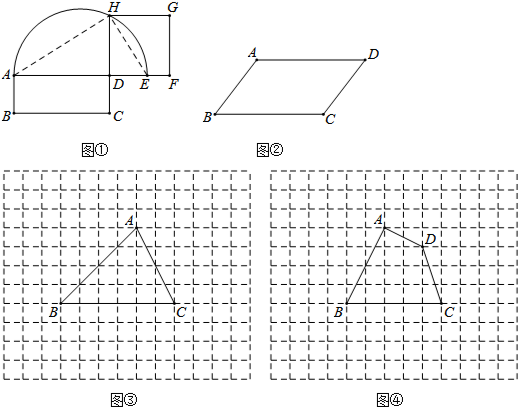
如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连接AH,EH.
∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.
∵DH⊥AE,∴∠ADH=∠EDH=90°
∴∠HAD+∠AHD=90°
∴∠AHD=∠HED,∴△ADH∽___.
∴
=
,即DH2=AD×DE.
又∵DE=DC
∴DH2=___,即正方形DFGH与矩形ABCD等积.
(2)操作实践
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图②,请用尺规作图作出与▱ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
(3)解决问题
三角形的“化方”思路是:先把三角形转化为等积的___(填写图形名称),再转化为等积的正方形.
如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n-1边形,…,直至转化为等积的三角形,从而可以化方.
如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).
(1)阅读填空
如图①,已知矩形ABCD,延长AD到E,使DE=DC,以AE为直径作半圆.延长CD交半圆于点H,以DH为边作正方形DFGH,则正方形DFGH与矩形ABCD等积.
理由:连接AH,EH.
∵AE为直径,∴∠AHE=90°,∴∠HAE+∠HEA=90°.
∵DH⊥AE,∴∠ADH=∠EDH=90°
∴∠HAD+∠AHD=90°
∴∠AHD=∠HED,∴△ADH∽___.
∴
| AD |
| DH |
| DH |
| DE |
又∵DE=DC
∴DH2=___,即正方形DFGH与矩形ABCD等积.
(2)操作实践
平行四边形的“化方”思路是,先把平行四边形转化为等积的矩形,再把矩形转化为等积的正方形.
如图②,请用尺规作图作出与▱ABCD等积的矩形(不要求写具体作法,保留作图痕迹).
(3)解决问题
三角形的“化方”思路是:先把三角形转化为等积的___(填写图形名称),再转化为等积的正方形.
如图③,△ABC的顶点在正方形网格的格点上,请作出与△ABC等积的正方形的一条边(不要求写具体作法,保留作图痕迹,不通过计算△ABC面积作图).
(4)拓展探究
n边形(n>3)的“化方”思路之一是:把n边形转化为等积的n-1边形,…,直至转化为等积的三角形,从而可以化方.
如图④,四边形ABCD的顶点在正方形网格的格点上,请作出与四边形ABCD等积的三角形(不要求写具体作法,保留作图痕迹,不通过计算四边形ABCD面积作图).

▼优质解答
答案和解析
(1)如图①,连接AH,EH,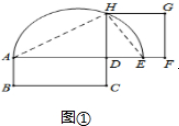
∵AE为直径,
∴∠AHE=90°,
∴∠HAE+∠HEA=90°.
∵DH⊥AE,
∴∠ADH=∠EDH=90°,
∴∠HAD+∠AHD=90°,
∴∠AHD=∠HED,
∴△ADH∽△HDE.
∴
=
,
即DH2=AD×DE.
又∵DE=DC,
∴DH2=AD×DC,
即正方形DFGH与矩形ABCD等积.
(2)作法:
①过A、D作AN、DM分别垂直BC于N、M;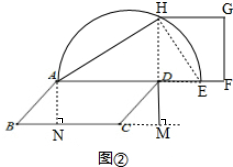
②延长AD,取DE=DM;
③以AE为直径作半圆O;
④延长MD交半圆O于H;
⑤以H、D作正方形HDFG,则正方形HDFG为平行四边形ABCD的等积正方形.
证明:
∵矩形ADMN的长和宽分别等于平行四边形ABCD的底和高,
∴矩形ADMN的面积等于平行四边形ABCD的面积,
∵AE为直径,
∴∠AHE=90°,
∴∠HAE+∠HEA=90°.
∵DH⊥AE,
∴∠ADH=∠EDH=90°,
∴∠HAD+∠AHD=90°,
∴∠AHD=∠HED,
∴△ADH∽△HDE.
∴
=
,
即DH2=AD×DE.
又∵DE=DM,
∴DH2=AD×DM,
即正方形DFGH与矩形ABMN等积,
∴正方形DFGH与平行四边形ABCD等积.
(3)作法:
①过A点作AD垂直BC于D;
②作AD的垂直平分线,取AD中点E;
③过E作BC平行线,作长方形BCGF,则S矩形BCGF=S△ABC;
其他步骤同(2)可作出其等积正方形.
(4)作法: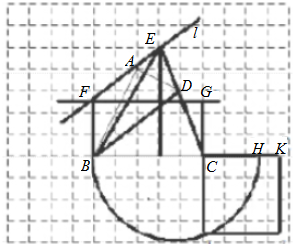
①过A点作BD平行线l;
②延长CD交平行线与E点;
③连接BE,则S四边形ABCD=S△EBC,
同(3)可作出其等积正方形.
△BCE与四边形ABCD等积,理由如下:
∵BD∥l,
∴S△ABD=S△EBD,
∴S△BCE=S四边形ABCD,
即△EBC与四边形ABCD等积.
故答案为:△HDE、AD×DC、矩形.

∵AE为直径,
∴∠AHE=90°,
∴∠HAE+∠HEA=90°.
∵DH⊥AE,
∴∠ADH=∠EDH=90°,
∴∠HAD+∠AHD=90°,
∴∠AHD=∠HED,
∴△ADH∽△HDE.
∴
| AD |
| DH |
| DH |
| DE |
即DH2=AD×DE.
又∵DE=DC,
∴DH2=AD×DC,
即正方形DFGH与矩形ABCD等积.
(2)作法:
①过A、D作AN、DM分别垂直BC于N、M;

②延长AD,取DE=DM;
③以AE为直径作半圆O;
④延长MD交半圆O于H;
⑤以H、D作正方形HDFG,则正方形HDFG为平行四边形ABCD的等积正方形.
证明:
∵矩形ADMN的长和宽分别等于平行四边形ABCD的底和高,
∴矩形ADMN的面积等于平行四边形ABCD的面积,
∵AE为直径,
∴∠AHE=90°,
∴∠HAE+∠HEA=90°.
∵DH⊥AE,
∴∠ADH=∠EDH=90°,
∴∠HAD+∠AHD=90°,
∴∠AHD=∠HED,
∴△ADH∽△HDE.
∴
| AD |
| DH |
| DH |
| DE |
即DH2=AD×DE.
又∵DE=DM,
∴DH2=AD×DM,
即正方形DFGH与矩形ABMN等积,
∴正方形DFGH与平行四边形ABCD等积.

(3)作法:
①过A点作AD垂直BC于D;
②作AD的垂直平分线,取AD中点E;
③过E作BC平行线,作长方形BCGF,则S矩形BCGF=S△ABC;
其他步骤同(2)可作出其等积正方形.
(4)作法:
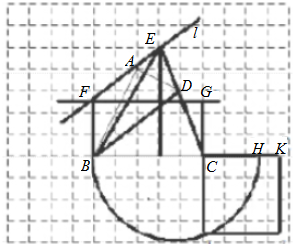
①过A点作BD平行线l;
②延长CD交平行线与E点;
③连接BE,则S四边形ABCD=S△EBC,
同(3)可作出其等积正方形.
△BCE与四边形ABCD等积,理由如下:
∵BD∥l,
∴S△ABD=S△EBD,
∴S△BCE=S四边形ABCD,
即△EBC与四边形ABCD等积.
故答案为:△HDE、AD×DC、矩形.
看了 设ω是一个平面图形,如果用直...的网友还看了以下:
seehowpeopleinteractsocially翻译是“观察人们如何交际”,可我直观的看是 2020-06-05 …
小李将100张卡摞起来,他从最上面的一张按如下的顺序进行操作:把最上面的一张卡片舍去,把下面一张卡 2020-06-06 …
加工中心走外圆我到现在还不明白怎么走外圆,比如一根水管,里面是是内圆,外面是外圆,而我现在需要加工 2020-06-08 …
我现在急需要一些还原问题,还要有过程.类似与下面这道:某数如果先加上3,再乘以3,然后除以2,最后 2020-06-08 …
已知一个平面与三维坐标系的三个平面的夹角度数,如何在三维坐标系中做出这个平面?这样的平面理论上是无 2020-06-14 …
怎样理解莫比乌斯环?莫比乌斯环资料描述它是一种单侧、不可定向的曲面.也就是说它没有正反面.这样的话 2020-06-22 …
正方体分割找规律将一个正方体图上颜色,把正方体的棱2等分,然后再沿等分线把正方体切开,这样就有8个 2020-06-30 …
地理如何分东西我都要疯了……譬如说画一个数轴,中间是0度经线,左右是180度经线,这样,如果A在0 2020-07-01 …
我用点棉花在耳朵里面掏不出来了怎么办呢??我用牙签裹住一点棉花来在耳朵里止痒结果掉里面了很深我自己 2020-07-06 …
英语翻译如果只有这样如果只有这样,你才不会拒绝我的靠近;如果只有这样,你才不会忘记我的存在;如果只有 2021-01-14 …