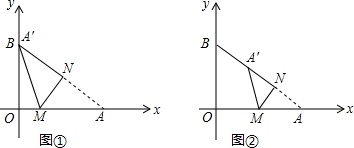
将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(4,0),点B(0,3),点O(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′
将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(4,0),点B(0,3),点O(0,0).过边OA上的动点M(点M不与点O,A重合)作MN丄AB于点N,沿着MN折叠该纸片,得顶点A的对应点A′.
(1)如图①,当点A′与顶点B重合时,求点M的坐标;
(2)如图②,当动点M运动到边AO的中点时,求点O与点A′的距离.
答案和解析
(1)∵点A(4,0),点B(0,3),
∴OA=4,OB=3,
∴AB=
=5,
由折叠的性质得:AN=BN=AB=2.5,∠ANM=90°=∠AOB,
∵∠NAM=∠OAB,
∴△AMN∽△ABO,
∴=,
即=,
解得:AM=,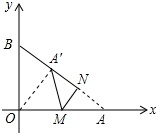
∴OM=OA-AM=4-=,
∴M(,0);
(2)连接OA′,如图所示:
∵M是AO的中点,
∴AM=OM=2,
由(1)得:△AMN∽△ABO,
∴=,即=,
解得:AN=,
由折叠的性质得:A′N=AN=,
∴A′A=,MN是△OAA′的中位线,
∴MN∥OA′,∠AA′O=∠ANM=90°,
∴OA′===.
1、求过点(0,-4)且倾斜角为直线(√3)x+y+3=0的倾斜角的一半的直线l的方程.2、直线m 2020-04-11 …
已知:抛物线y=-x^2-(m-4)x+3(m-1)与x轴交于A,B两点,与y轴交于点D(1)若△ 2020-05-14 …
若一个正数的平方根分别是2m-2与m-4,则m为()A.-2B.1C.2D.-2或2 2020-05-15 …
如果5m+4/1与m+4/1互为相反数,那么m的值为多少 2020-05-16 …
在平面直角坐标系中直线y=x+4与x轴交与点A,与y轴交与点B,且反比例函数y=m-8/x交与点C 2020-05-17 …
在平面直角坐标系中,直线y=x+4与x轴交与点A,与y轴交与点B,且反比例函数y=m-8/x交与点 2020-05-17 …
已知a=(1,2),b=(m,-1)\x0c(1)若a与b的夹角为3/4派,求m的值?\x0c(2 2020-06-27 …
x²/m+2+y²/3-m=1设m=2,过点D(0,4)的直线l与曲线C交与M,.N两点,O为坐标 2020-06-27 …
若一元二次方程ax的平方=b(ab>0)的两个根分别是2m-1与m+4 2020-11-12 …
若一元二次方程ax的平方=b(ab>0)的两个根分别是2m-1与m+4,则a分之b是多少是2m-4和 2020-11-12 …



