早教吧作业答案频道 -->数学-->
如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).(1)求这个二次函数的表达式;(2)在抛物线的对称轴上是否存在一点P,使得|PA-PC|的值最大?若存在,
题目详情
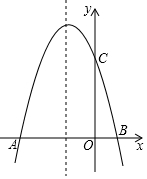
如图,已知二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4).
(1)求这个二次函数的表达式;
(2)在抛物线的对称轴上是否存在一点P,使得|PA-PC|的值最大?若存在,求出P点坐标;若不存在,请说明理由.
(3)在平面直角坐标系内,是否存在点Q,使A,B,C,Q四点构成平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.

(1)求这个二次函数的表达式;
(2)在抛物线的对称轴上是否存在一点P,使得|PA-PC|的值最大?若存在,求出P点坐标;若不存在,请说明理由.
(3)在平面直角坐标系内,是否存在点Q,使A,B,C,Q四点构成平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.
▼优质解答
答案和解析
(1)∵二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4),
∴
,解得
,
∴二次函数的表达式为y=-x2-3x+4;
(2)∵y=-x2-3x+4,
∴对称轴为x=-
,
∵A(-4,0),
∴B(1,0),
∵P在对称轴上,
∴PA=PB,
∴|PA-PC|=|PB-PC|≤BC,即当P、B、C三点在一条线上时|PA-PC|的值最大,
设直线BC解析式为y=kx+b,
∴
,解得
,
∴直线BC解析式为y=-4x+4,
令x=-
可得y=-4×(-
)+4=10,
∴存在满足条件的点P,其坐标为(-
,10);
(3)存在点Q,使A,B,C,Q四点构成平行四边形,
理由:①以AB为边时,则有CQ∥AB,即点Q的纵坐标为4,
∵CQ=AB=5,且C(0,4),
∴Q(-5,4)或(5,4),
②以AB为对角线时,CQ必过线段AB中点,且被AB平分,即:AB的中点也是CQ的中点,
∵A、B中点坐标为(-
,0),且C(0,4),
∴Q点横坐标=2×(-
)-0=-3,Q点纵坐标=0-4=-4,
∴Q(-3,-4),
综合可知存在满足条件的点D,坐标为(-5,4)或(5,4)或(-3,-4).
(1)∵二次函数y=-x2+bx+c的图象交x轴于点A(-4,0)和点B,交y轴于点C(0,4),
∴
|
|
∴二次函数的表达式为y=-x2-3x+4;
(2)∵y=-x2-3x+4,
∴对称轴为x=-
| 3 |
| 2 |
∵A(-4,0),
∴B(1,0),
∵P在对称轴上,
∴PA=PB,
∴|PA-PC|=|PB-PC|≤BC,即当P、B、C三点在一条线上时|PA-PC|的值最大,
设直线BC解析式为y=kx+b,
∴
|
|
∴直线BC解析式为y=-4x+4,
令x=-
| 3 |
| 2 |
| 3 |
| 2 |
∴存在满足条件的点P,其坐标为(-
| 3 |
| 2 |
(3)存在点Q,使A,B,C,Q四点构成平行四边形,
理由:①以AB为边时,则有CQ∥AB,即点Q的纵坐标为4,
∵CQ=AB=5,且C(0,4),
∴Q(-5,4)或(5,4),
②以AB为对角线时,CQ必过线段AB中点,且被AB平分,即:AB的中点也是CQ的中点,
∵A、B中点坐标为(-
| 3 |
| 2 |
∴Q点横坐标=2×(-
| 3 |
| 2 |
∴Q(-3,-4),
综合可知存在满足条件的点D,坐标为(-5,4)或(5,4)或(-3,-4).
看了 如图,已知二次函数y=-x2...的网友还看了以下:
二次函数y =ax^2+bx的图像如图,若一元二次方程ax^2+bx二次函数y=ax^2+bx的图 2020-04-05 …
若关于x的多项式-2x的二次方+ax+bx的二次方-5x-1的值与x无关,求a+b的值 2020-05-16 …
阅读材料;把形如ax的平方+bx+c的二次二项式(或其一部分)配成完全平方式的方法叫做配方法,配方 2020-06-26 …
已知关于x的二次函数y=ax2+bx+c(a>0)的图象经过点C(0,1),已知关于x的二次函数y 2020-07-23 …
什么是二次三项式,如ax^2+bx+c,a,b,c是常数,x是未知数,当a=0是,远视变为一次二项 2020-07-31 …
关于x的二次三项式ax2+bx+c,满足下表中的对应关系:x…-5-4-2-101245…ax2+ 2020-07-31 …
当a,b,c满足什么条件时,方程(a-1)x2-bx+c=0是一元二次方程?这时方程的二次项系数、 2020-08-01 …
(带余除法)m取什么值时,分式2m+7/m-1的值是正整数已知:ax的三次方+bx的二次方+cx+ 2020-08-02 …
关于x的二元三项式ax²+bx+c(a不等于零)的因式分解中的概念问题书上说:若关于x的方程ax²+ 2020-11-07 …
还是关于x的二元三项式ax²+bx+c(a不等于零)的因式分解中的概念问题不好意思继续提问下:韦达定 2020-11-07 …