早教吧作业答案频道 -->数学-->
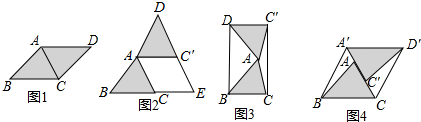
综合与实践问题情境在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(∠BAC>90°)沿对角线AC剪开,得到△ABC和△ACD.操作发现
题目详情
综合与实践
问题情境
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(∠BAC>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现
(1)将图1中的△ACD以A为旋转中心,逆时针方向旋转α,使α=∠BAC,得到如图2所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是___;
(2)将图1中的△ACD以A为旋转中心,按逆时针方向旋转△AC′D,使α=2∠BAC,得到如图3所示的△AC′D,连接DB,C′C,得到四边形BCC′D,发现它是矩形,请你证明这个结论;
(3)请你参照以上操作,将图1中的△ACD在同一平面内进行一次平移,得到△A′C′D′,在图4中画出平移后构造出的新图形,标明字母,说明平移的方法,并写出你发现的结论(不必证明).
问题情境
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(∠BAC>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现
(1)将图1中的△ACD以A为旋转中心,逆时针方向旋转α,使α=∠BAC,得到如图2所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是___;
(2)将图1中的△ACD以A为旋转中心,按逆时针方向旋转△AC′D,使α=2∠BAC,得到如图3所示的△AC′D,连接DB,C′C,得到四边形BCC′D,发现它是矩形,请你证明这个结论;
(3)请你参照以上操作,将图1中的△ACD在同一平面内进行一次平移,得到△A′C′D′,在图4中画出平移后构造出的新图形,标明字母,说明平移的方法,并写出你发现的结论(不必证明).

▼优质解答
答案和解析
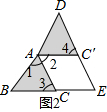 (1)如图2,由题意可得:∠1=∠2,∠2=∠3,∠1=∠4,AC=AC′,
(1)如图2,由题意可得:∠1=∠2,∠2=∠3,∠1=∠4,AC=AC′,
∴AC′∥EC,AC∥C′E,
∴四边形ACEC′是平行四边形,
∴四边形ACEC′是菱形;
故答案为:菱形;
(2)证明:如图3,作AE⊥CC′于点E,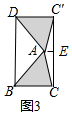
由旋转得:AC′=AC,
∴∠CAE=∠C′AE=
α=∠BAC,AE⊥CC',
∵四边形ABCD是菱形,
∴BA=BC,
∴∠BCA=∠BAC,
∴∠CAE=∠BCA,
∴AE∥BC,
同理可得:AE∥DC′,
∴BC∥DC′,
∴∠BCC′=90°,
又∵BC=DC′,
∴四边形BCC′D是平行四边形,
∵∠BCC′=90°,
∴四边形BCC′D是矩形;
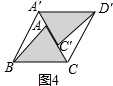
(3)如图4,将△ACD沿着射线CA方向平移,平移距离为
AC的长度,得到△A′C′D′,连接A′B,D′C,则四边形BCD'A'是平行四边形.答案不唯一.
理由:∵BC=A′D′,BC∥A′D′,
∴四边形A′BCD′是平行四边形.
 (1)如图2,由题意可得:∠1=∠2,∠2=∠3,∠1=∠4,AC=AC′,
(1)如图2,由题意可得:∠1=∠2,∠2=∠3,∠1=∠4,AC=AC′,∴AC′∥EC,AC∥C′E,
∴四边形ACEC′是平行四边形,
∴四边形ACEC′是菱形;
故答案为:菱形;
(2)证明:如图3,作AE⊥CC′于点E,

由旋转得:AC′=AC,
∴∠CAE=∠C′AE=
| 1 |
| 2 |
∵四边形ABCD是菱形,
∴BA=BC,
∴∠BCA=∠BAC,
∴∠CAE=∠BCA,
∴AE∥BC,
同理可得:AE∥DC′,
∴BC∥DC′,
∴∠BCC′=90°,
又∵BC=DC′,
∴四边形BCC′D是平行四边形,
∵∠BCC′=90°,
∴四边形BCC′D是矩形;

(3)如图4,将△ACD沿着射线CA方向平移,平移距离为
| 1 |
| 2 |
理由:∵BC=A′D′,BC∥A′D′,
∴四边形A′BCD′是平行四边形.
看了 综合与实践问题情境在综合与实...的网友还看了以下:
张老师要做60个底是6厘米,高是4厘米的直角三角形学具,需要长和宽分别为多大的纸需要长和宽分别为多 2020-05-09 …
张老师要做60个底是6厘米,高是4厘米的直角三角形学具,应选()纸A长80厘米,宽9厘米的长方形B 2020-05-09 …
一种用塑料围成的等腰三角形学具,已知它的俩条边长分别是10厘米,5厘米,做3个学具需要塑料棒多长 2020-05-14 …
冬冬用一张边长16.5厘米的正方形纸剪三角形学具,能剪出多少个直角边是5厘米的等腰直角三角形数学题 2020-05-22 …
冬冬用一张边长15.2cm的正方形纸剪三角形学具,能剪出多少个直角边是5cm的等腰直角三角形? 2020-05-22 …
如何准确找出相似三角形的对应点在初三的学习中,相似三角形学的很不好!对应关系,对应点找不准,一直下 2020-07-04 …
H2O分子中O原子采取不等性SP3杂化,分子在空间的构型为?A,角形B,三角型C,四面体D,三角锥 2020-07-05 …
东东用一张边长为16.5cm的正方形纸剪三角形学具,能剪出多少个直角边是5cm的等腰直角三角形? 2020-07-15 …
为什么我几何三角形学的好,圆学的不好,圆总是找不准点,三角形就学的很好, 2020-11-04 …
我儿子上中班教什么总是教不会,形状,三角形圆形长方形,说了长方形就不知三角形...,学其他也不例外 2020-11-28 …