一个多面体的三视图和直观图如图所示，其中D为AA1的中点．（1）求平面B1DC把多面体ABC-A1B1C1分成两部分的体积之比；（2）在线段B1C上是否存在一点E，使A1E∥平面BDC，若存

Question

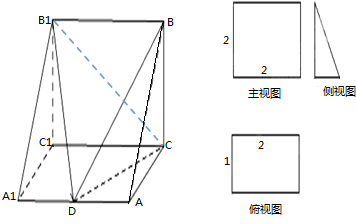
一个多面体的三视图和直观图如图所示，其中D为AA ₁ 的中点．
（1）求平面B ₁ DC把多面体ABC-A ₁ B ₁ C ₁ 分成两部分的体积之比；
（2）在线段B ₁ C上是否存在一点E，使A ₁ E∥平面BDC，若存在，指出E点的位置，若不存在，请说明理由；
（3）求直线BD与平面B ₁ DC夹角的正弦值．

Answer 1

考点：
直线与平面所成的角 棱柱、棱锥、棱台的体积 直线与平面平行的判定
专题：
空间位置关系与距离 空间角
分析：
（1）由三视图知直观图为直三棱柱，且底ABC中，BC⊥AC，BC=CC1=2，AC=1，由此能求出平面B1DC把多面体ABC-A1B1C1分成两部分的体积之比．（2）取B1C的中点E，BC中点F，连EF，A1E，DF，由已知得A1DEF为平行四边形，由此能求出在线段B1C上存在一点E，使A1E∥平面BDC，此时E为线段B1C中点．（3）连结C1D，由题意得CD⊥C1D，从而CD⊥面B1C1D，作C1M⊥B1D，则C1M⊥面B1DC，由此能求出直线BD与平面B1DC夹角的正弦值．

（1）由三视图知直观图为直三棱柱，且底ABC中，BC⊥AC，BC=CC1=2，AC=1，∴VB1-A1DCC1=13SA1DCC1?B1C1=13×(1+2)2×2=1，VABC-A1B1C1=S△ABC?AA1=12×2×1×2=2，∴平面B1DC把多面体ABC-A1B1C1分成两部分的体积之比为1：1．（2）取B1C的中点E，BC中点F，连EF，A1E，DF，由已知得A1DEF为平行四边形，∴A1E∥DF，而DF?面BDC，A1E?面BDC，∴A1E∥面BDC，∴在线段B1C上存在一点E，使A1E∥平面BDC，此时E为线段B1C中点．（3）连结C1D，由题意得CD⊥C1D，又CD⊥B1C1，∴CD⊥面B1C1D，∴面B1DC⊥面B1C1D，作C1M⊥B1D，则C1M⊥面B1DC，∴面B1DC⊥面B1C1D，作C1M⊥B1D，则C1M⊥面B1DC，由题意得C1M=233，即B点到平面B1DC的距离为233，设直线BD与平面B1DC夹角为θ，∵BD=6，∴sinθ=C1MBD=2336=23．∴直线BD与平面B1DC夹角的正弦值为23．
点评：
本题考查空间线面关系、几何体的体积等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．