早教吧作业答案频道 -->数学-->
已知,棱长为2的正方体内有一内接四面体A-BCD,且B,C分别为正方体某两条棱的中点,其三视图如图所示:(Ⅰ)求证:AD⊥BC;(Ⅱ)求四面体A-BCD的体积.
题目详情
已知,棱长为2的正方体内有一内接四面体A-BCD,且B,C分别为正方体某两条棱的中点,其三视图如图所示:
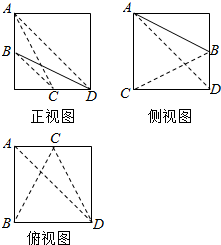
(Ⅰ)求证:AD⊥BC;
(Ⅱ)求四面体A-BCD的体积.

(Ⅰ)求证:AD⊥BC;
(Ⅱ)求四面体A-BCD的体积.
▼优质解答
答案和解析
(Ⅰ)证明:由已知中的三视图,可得A,B,C,D四点位置如下图所示:
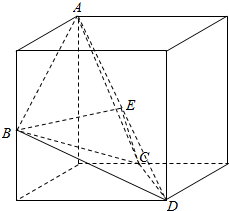
∵正方体的棱长为2,故AB=BD=AC=CD=
,AD=2
,BC=
,
令E为AD的中点,连接BE,CE,
则BE⊥AD,CE⊥AD,
则AD⊥平面BCE,
∴AD⊥BC;
(Ⅱ) 由勾股定理可得:BE=CE=
,
由海伦公式平面BCE的面积S=
,
又由AD=2
,
故四面体A-BCD的体积V=
×
×2
=1.

∵正方体的棱长为2,故AB=BD=AC=CD=
| 5 |
| 3 |
| 6 |
令E为AD的中点,连接BE,CE,
则BE⊥AD,CE⊥AD,
则AD⊥平面BCE,
∴AD⊥BC;
(Ⅱ) 由勾股定理可得:BE=CE=
| 2 |
由海伦公式平面BCE的面积S=
| ||
| 2 |
又由AD=2
| 3 |
故四面体A-BCD的体积V=
| 1 |
| 3 |
| ||
| 2 |
| 3 |
看了 已知,棱长为2的正方体内有一...的网友还看了以下:
有哪六种普通晶体体系?(如立方体形状晶体、四方体形状晶体等) 2020-04-27 …
什么叫长方体互不相邻的顶点长方体互不相邻的四个顶点,是哪四个最好画图标注………………有加分 2020-05-13 …
高一立体几何证明题:正方体ABCD-A1B1C1D1中,点O为BD中点正方体ABCD-A1B1C1 2020-05-16 …
球体的重心,内接立方体的一个顶点,立方体的重心在不在一条直线上? 2020-06-04 …
长方体哪些面完全相同长方体有(6)个面.()的面完全相同.有(12)条棱,(不知道啊)的棱完全相等 2020-06-19 …
ug7.0点长方体按钮画长方体,如果画的长度很长时画出来的就是空的,怎么弄呢? 2020-06-29 …
什么叫长方体的顶点,长方体有多少个顶点我们老师布置的,我们还没学那 2020-07-30 …
有个四方体每面从每面看都有10根柱子,问这个四方体一共有多少根柱子, 2020-11-07 …
(急)不规则立方体计算方法.已知条件如下,已知一个四方体的上表面积跟下表面积相等,但是四方体上表面积 2020-11-07 …
求算四方形容积多少升?一个四方形高370MM宽230MM厚138MM我想请问下这个四方体的有多少升 2020-11-07 …