已知e1，e2，e3是空间的一个基底，试问向量a＝3e1＋2e2＋e3，b＝－e1＋e2＋3e3，c＝2e1－e2－4e3是否共面？并说明理由．

Question

已知e₁，e₂，e₃是空间的一个基底，试问向量a＝3e₁＋2e₂＋e₃，b＝－e₁＋e₂＋3e₃，c＝2e₁－e₂－4e₃是否共面？并说明理由．

Answer 1

解　由共面向量定理可知，关键是能否找到三个不全为零的实数x，y，z，使得xa＋yb＋zc＝0，即x(3e₁＋2e₂＋e₃)＋y(－e₁＋e₂＋3e₃)＋z(2e₁－e₂－4e₃)＝0.亦即(3x－y＋2z)e₁＋(2x＋y－z)e₂＋(x＋3y－4z)e₃＝0.

由于e₁，e₂，e₃不共面，

故得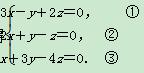

①＋②求得z＝－5x，代入③得y＝－7x，取x＝－1，

则y＝7，z＝5，于是－a＋7b＋5c＝0，即a＝7b＋5c，所以a，b，c三向量共面．