早教吧作业答案频道 -->数学-->
如图,圆E是三角形ABC的外接圆,∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.(1)求三角形ABC的外接圆直径;(2)求过ABC三点的抛物线的解析式;(3)设P是(2)中抛
题目详情
如图,圆E是三角形ABC的外接圆,∠BAC=45°,AO⊥BC于O,且BO=2,CO=3,分别以BC、AO所在直线建立x轴.
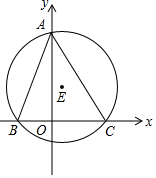
(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程)

(1)求三角形ABC的外接圆直径;
(2)求过ABC三点的抛物线的解析式;
(3)设P是(2)中抛物线上的一个动点,且三角形AOP为直角三角形,则这样的点P有几个?(只需写出个数,无需解答过程)
▼优质解答
答案和解析
(1)如图1中,连接EB、EC.
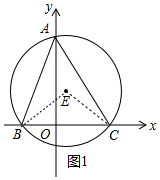
∵BC=OB+OC=5,∠BEC=2∠BC=90°,
∴EB=EC=
,
∴ E的直径为5
.
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.
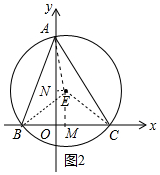
在Rt△EMC中,EM=ON=
=
=
,OM=NE=OC-CM=
,
在Rt△EN中,AN=
=
=
,
∴OA=AN+ON=6,
∴A(0,6),B(-2,0),C(3,0),
设抛物线的解析式为y=a(x+2)(x-3),把(0,6)的坐标代入得a=-1,
∴抛物线的解析式为y=-x2+x+6.
(3)如图3中,
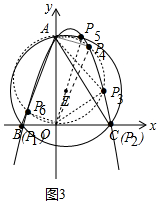
①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.
②当PA⊥OA时,有一�

∵BC=OB+OC=5,∠BEC=2∠BC=90°,
∴EB=EC=
5
| ||
| 2 |
∴ E的直径为5
| 2 |
(2)如图2中,作EM⊥BC于M,EN⊥OA于N,连接AE,则四边形EMON是矩形.

在Rt△EMC中,EM=ON=
| EC2-CM2 |
(
|
| 5 |
| 2 |
| 1 |
| 2 |
在Rt△EN中,AN=
| AE2-EN2 |
(
|
| 7 |
| 2 |
∴OA=AN+ON=6,
∴A(0,6),B(-2,0),C(3,0),
设抛物线的解析式为y=a(x+2)(x-3),把(0,6)的坐标代入得a=-1,
∴抛物线的解析式为y=-x2+x+6.
(3)如图3中,

①以OA为直径画圆与抛物线有4个交点,根据直径所对的圆周角是直角,可知这样有4个点P满足条件.
②当PA⊥OA时,有一�
看了 如图,圆E是三角形ABC的外...的网友还看了以下:
下列说法正确的是()①三角形的三条中线都在三角形内部;②三角形的三条角平分线都在三角形内部;③三角 2020-06-21 …
一个三角形的三个角分别是95度、25度、60度,这个三角形是()A.锐角三角形B.直角三角形C.钝 2020-07-17 …
三角形的三条角平分线相交于三角形一点三角形的三条高相交于一线的位置情况有三种:如果是钝角三角形,那 2020-07-30 …
锐角三角形的三个角都是角;直角三角形中必定有一个是角;钝角三角形中也必定有一个角是角. 2020-07-30 …
三角形:三角形的三条中线相交于一点,交点在三角形部三角形的三条角平分线交于一点,交点在三角形部锐角 2020-08-02 …
三角形的三个角中有一个角是91度,这个三角形是()A.锐角三角形B.钝角三角形C.直角三角形 2020-08-03 …
猜一猜.信封里放的是什么三角形?(1)三角形的一个角是钝角,这个三角形是.(2)三角形的三个角都是 2020-08-03 …
猜一猜.信封里放的是什么三角形?(1)三角形的一个角是钝角,这个三角形是.(2)三角形的三个角猜一 2020-08-03 …
锐角三角形的三个角都是角;有个角是直角的三角形叫做直角三角形;有一个角是角的三角形叫做钝角三角形. 2020-08-03 …
三个角相等的三角形是等边三角形.的逆命题为什么不是等边三角形是3个角相等的三角形呢等边三角形的三个 2020-08-03 …