早教吧作业答案频道 -->数学-->
问题探究(1)如图1,点E为矩形ABCD内一点,请过点E作一条直线,将矩形ABCD的面积分为相等的两部分;(2)如图2,在矩形ABCD中,AB=8,BC=6,P为对角线AC上一点,且AC=3AP,请问在边CD上是否存
题目详情
问题探究
(1)如图1,点E为矩形ABCD内一点,请过点E作一条直线,将矩形ABCD的面积分为相等的两部分;
(2)如图2,在矩形ABCD中,AB=8,BC=6,P为对角线AC上一点,且AC=3AP,请问在边CD上是否存在一点E,使得直线PE将矩形ABCD的面积分为2:3两部分,如果存在求出DE的长;如果不存在,请说明理由;
解决问题
(3)如图3,现有一块矩形空地ABCD,AB=80米,BC=60米,P为对角线AC上一点,且PC=3AP,计划在这块空地上修建一个四边形花园AECF,使得E、F分别在线段AD、AB上,且EF经过点P,若每平方米的造价为100元,请求出修建该花园所需费用的范围(其他费用不计).
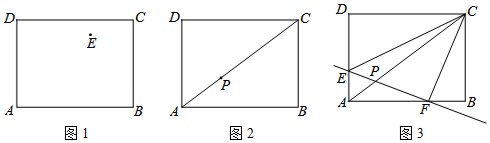
(1)如图1,点E为矩形ABCD内一点,请过点E作一条直线,将矩形ABCD的面积分为相等的两部分;
(2)如图2,在矩形ABCD中,AB=8,BC=6,P为对角线AC上一点,且AC=3AP,请问在边CD上是否存在一点E,使得直线PE将矩形ABCD的面积分为2:3两部分,如果存在求出DE的长;如果不存在,请说明理由;
解决问题
(3)如图3,现有一块矩形空地ABCD,AB=80米,BC=60米,P为对角线AC上一点,且PC=3AP,计划在这块空地上修建一个四边形花园AECF,使得E、F分别在线段AD、AB上,且EF经过点P,若每平方米的造价为100元,请求出修建该花园所需费用的范围(其他费用不计).

▼优质解答
答案和解析
(1)如图1中,
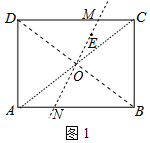
连接AC、BD交于点O,作直线EO,直线EO将矩形ABCD的面积分为相等的两部分.
理由:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠MCO=∠NAO,
在△MCO和△NAO中,
,
△MCO≌△NAO,
∴S△MCO=S△NAO,
∵S△ADC=S△ABC,
∴S四边形ANMD=S四边形BCMN.
(2)如图2中,作MN∥BC,使得四边形BCMN的面积=
四边形ABCD的面积,
连接AM、DN交于点O,作直线OP交CD于E,交AB于H,此时四边形ADEH的面积:四边形BCEH的面积=2:3.
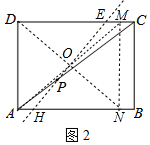
易知:CM=BN=
,DM=AN=
,
由△EOM≌△HAO,得到AH=EM,设AH=EM=x,
∵AH∥EC,
∴
=
=
,
∴
=
,
解得x=
,
∴DE=DM-EM=
-
=
.
(3)如图3中,连接BD交AC于O,作OM⊥AD于M,ON⊥AN于N.
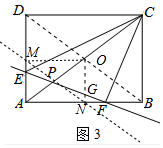
∵PC=3AO,OA=OC,
∴OP=OA,
∴过点P的任意直线将矩形ANOM的面积平分,
∵PC=3AP,
∴S△EPC=3S△EAP,
S△PCF=3S△APF,
∴S四边形AECF=4S△AEF,
当直线EF与对角线MN重合时,△AEF的面积最小(△AEF的面积=
矩形AMON的面积+△FNG的面积,所以△AEF的面积>△AMN的面积),最小值=
矩形AMON的面积=600m2,
∴四边形AECF的面积的最小值为2400m2,
当点F与点B重合时,△NGF的面积最大,此时AE=
BC=20,
∴此时△AEF的面积最大,最大面积=
×80×20=800m2,
四边形AECF的面积的最大值为3200m2,
∵每平方米的造价为100元
∴修建该花园所需费用w的范围为240000元≤w≤320000元.

连接AC、BD交于点O,作直线EO,直线EO将矩形ABCD的面积分为相等的两部分.
理由:∵四边形ABCD是矩形,
∴AB∥CD,OA=OC,
∴∠MCO=∠NAO,
在△MCO和△NAO中,
|
△MCO≌△NAO,
∴S△MCO=S△NAO,
∵S△ADC=S△ABC,
∴S四边形ANMD=S四边形BCMN.
(2)如图2中,作MN∥BC,使得四边形BCMN的面积=
| 1 |
| 5 |
连接AM、DN交于点O,作直线OP交CD于E,交AB于H,此时四边形ADEH的面积:四边形BCEH的面积=2:3.

易知:CM=BN=
| 8 |
| 5 |
| 32 |
| 5 |
由△EOM≌△HAO,得到AH=EM,设AH=EM=x,
∵AH∥EC,
∴
| AH |
| EC |
| AP |
| PC |
| 1 |
| 2 |
∴
| x | ||
x+
|
| 1 |
| 2 |
解得x=
| 8 |
| 5 |
∴DE=DM-EM=
| 32 |
| 5 |
| 8 |
| 5 |
| 24 |
| 5 |
(3)如图3中,连接BD交AC于O,作OM⊥AD于M,ON⊥AN于N.

∵PC=3AO,OA=OC,
∴OP=OA,
∴过点P的任意直线将矩形ANOM的面积平分,
∵PC=3AP,
∴S△EPC=3S△EAP,
S△PCF=3S△APF,
∴S四边形AECF=4S△AEF,
当直线EF与对角线MN重合时,△AEF的面积最小(△AEF的面积=
| 1 |
| 2 |
| 1 |
| 2 |
∴四边形AECF的面积的最小值为2400m2,
当点F与点B重合时,△NGF的面积最大,此时AE=
| 1 |
| 3 |
∴此时△AEF的面积最大,最大面积=
| 1 |
| 2 |
四边形AECF的面积的最大值为3200m2,
∵每平方米的造价为100元
∴修建该花园所需费用w的范围为240000元≤w≤320000元.
看了 问题探究(1)如图1,点E为...的网友还看了以下:
下图是四幅等高线地形示意图,能体现“深山藏古寺”意境的是()A.a图B.b图C.c图D.d图 2020-05-02 …
读“海口、吐鲁番、漠河、五道梁”四地气温及降水量变化图,完成1~3题1.上面四幅图中,代表漠河的是 2020-05-02 …
读“我国东部地区四城市气温曲线和降水量分配示意图”,完成11-12题.广州的气温和降水量分配图是( 2020-05-02 …
读我国“我国锋面雨带图”回答文题。小题1:在“我国锋面雨带图”中表示我国华南秋雨的图是()A.A图 2020-05-02 …
下图所示为12月22日A、B、C、D四地昼夜长短示意图,阴影代表黑夜,据图回答1—3题。1、水平运 2020-05-02 …
经过对某生物体内的核酸成分的化学分析得知,嘌呤占58%,嘧啶占42%,由此可以判断()A.此生物体 2020-06-07 …
经过对某生物体内的核酸成分的化学分析得知,嘌呤占58%,嘧啶占42%,由此可以判断()A.此生物体 2020-06-26 …
如图,D是等边三角形ABC中AC边的中点,E在BC的延长线上,DE=DB,若△ABC的周长为6,则 2020-06-27 …
对下列四幅教材中的图片的描述,正确的是()A.用不同的力敲同一个编钟,可以发出不同音调的声音B.上 2020-07-04 …
在一张不透光的纸上剪出一个方形扎,让太阳垂直射在纸上,光线通过方形孔在地面上形成的光斑形状A.一定 2020-07-08 …