早教吧作业答案频道 -->数学-->
在学习三角形中位线的性质时,小亮对课本给出的解集办法进行了认真思考:小亮发现:可能证法的实质是用中心对称的方法来构造全等三角形请你利用小亮的发现解决下列问题:(1)如图
题目详情
在学习三角形中位线的性质时,小亮对课本给出的解集办法进行了认真思考:
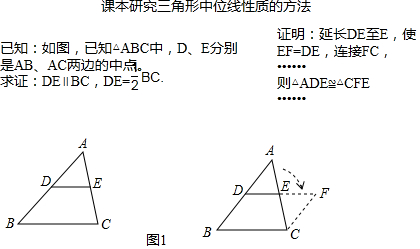
小亮发现:可能证法的实质是用中心对称的方法来构造全等三角形
请你利用小亮的发现解决下列问题:
(1)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程;
证明:
___.
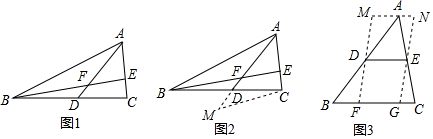
(2)解决问题:如图3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是___.

小亮发现:可能证法的实质是用中心对称的方法来构造全等三角形
请你利用小亮的发现解决下列问题:
(1)如图2,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF,求证:AC=BF.
请你帮助小亮写出辅助线作法并完成论证过程;
证明:
___.

(2)解决问题:如图3,在△ABC中,∠B=45°,AB=10,BC=8,DE是△ABC的中位线,过点D、E作DF∥EG,分别交BC于F、G,过点A作MN∥BC,分别与FD、GE的延长线交于M、N,则四边形MFGN周长的最小值是___.
▼优质解答
答案和解析
(1)延长AD至点M,使MD=FD,连接MC,
在△BDF和△CDM中,
,
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA,
∵∠AFE=∠BFM,
∴∠M=∠MAC,
∴AC=MC,
∴BF=AC;
故答案为:延长AD至点M,使MD=FD,连接MC,
在△BDF和△CDM中,
,
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA,
∵∠AFE=∠BFM,
∴∠M=∠MAC,
∴AC=MC,
∴BF=AC;
(2)如图,
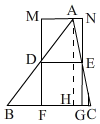
∵MN∥BC,FM∥GN,
∴四边形MFGN是平行四边形,
∴MF=NG,MN=FG,
∵DE是△ABC的中位线,
∴DE=
BC=4,DE∥BC,
∴MN=FG=
BC=4,
∴四边形MFGN周长=2(MF+FG)=2MF+8,
∴MF⊥BC时,MF最短,
即:四边形MFGN的周长最小,
过点A作AH⊥BC于H,
∴FM=AH
在Rt△ABH中,∠B=45°,AB=10,
∴AH=
=5
,
∴四边形MFGN的周长最小为2MF+8=10
+8.
故答案为10
+8.
在△BDF和△CDM中,
|
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA,
∵∠AFE=∠BFM,
∴∠M=∠MAC,
∴AC=MC,
∴BF=AC;
故答案为:延长AD至点M,使MD=FD,连接MC,
在△BDF和△CDM中,
|
∴△BDF≌△CDM(SAS).
∴MC=BF,∠M=∠BFM.
∵EA=EF,
∴∠EAF=∠EFA,
∵∠AFE=∠BFM,
∴∠M=∠MAC,
∴AC=MC,
∴BF=AC;
(2)如图,

∵MN∥BC,FM∥GN,
∴四边形MFGN是平行四边形,
∴MF=NG,MN=FG,
∵DE是△ABC的中位线,
∴DE=
| 1 |
| 2 |
∴MN=FG=
| 1 |
| 2 |
∴四边形MFGN周长=2(MF+FG)=2MF+8,
∴MF⊥BC时,MF最短,
即:四边形MFGN的周长最小,
过点A作AH⊥BC于H,
∴FM=AH
在Rt△ABH中,∠B=45°,AB=10,
∴AH=
| 10 | ||
|
| 2 |
∴四边形MFGN的周长最小为2MF+8=10
| 2 |
故答案为10
| 2 |
看了 在学习三角形中位线的性质时,...的网友还看了以下:
71又15/16×(-8)解法1:-1151×8=-9208/16=-575又1/271又15/1 2020-04-07 …
英语作文请你谈谈你在学习中遇到的问题及解决方法遇到的问题是1.休息时间少2.压力太大,厌倦学习3. 2020-06-08 …
英语翻译雅思写作技巧1.开头的写法(1)背景法:说明事件发生的时间、地点、情景等背景.(2)人物法 2020-06-23 …
近年来,我国颁布了一系列法律、法规来保护劳动者的合法权益,并积极采取多种措施以解决劳动者就业问题。 2020-07-06 …
根据所给材料回答问题1901年法国考古队在伊朗古城苏萨遗址发现一根黑色的玄武岩石柱,石柱上端是浮雕 2020-07-06 …
民法判断题1、依我国物权法规定,典权属于非典型担保物权2、所有权一般是无限期的,但法律规定或当事人约 2020-11-05 …
用简便方法计算下面各题(1)2又3分之2+(-3又4分之3)+(-2又3分之2)(2)-6.75+4 2020-11-25 …
初三概率题:1、人们常用模拟试验的方法估计事件发生的概率,常用的模拟方法有实物模拟和两种;2、... 2020-12-01 …
5年了,还是没人能说出下面幽默法的例子.真是好失望哦!其四,借题发挥法借题发挥就是借用别人的话题进行 2021-01-08 …
科学发展观的第一要义是发展;核心是以人为本;基本要求是全面协调可持续;根本方法是统筹兼顾。据此回答1 2021-02-08 …