早教吧作业答案频道 -->数学-->
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.(1)求抛物线的函数关系式;(2)设点P是直线l上的一个动点,当点P到点A、点B的
题目详情
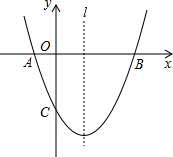
如图,已知抛物线y=ax2+bx+c(a≠0)经过A(-1,0)、B(3,0)、C(0,-3)三点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.

(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
▼优质解答
答案和解析
(1)将A(-1,0)、B(3,0)、C(0,-3)代入抛物线y=ax2+bx+c中,得:
,
解得:
故抛物线的解析式:y=x2-2x-3.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,
此时x=-
=1,
故P(1,0);
(3)如图所示:抛物线的对称轴为:x=-
=1,设M(1,m),已知A(-1,0)、C(0,-3),则:
MA2=m2+4,MC2=(3+m)2+1=m2+6m+10,AC2=10;
①若MA=MC,则MA2=MC2,得:
m2+4=m2+6m+10,解得:m=-1,
②若MA=AC,则MA2=AC2,得:
m2+4=10,得:m=±
;
③若MC=AC,则MC2=AC2,得:
m2+6m+10=10,得:m1=0,m2=-6;
当m=-6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,
)(1,-
)(1,-1)(1,0).
|
解得:
|
故抛物线的解析式:y=x2-2x-3.
(2)当P点在x轴上,P,A,B三点在一条直线上时,点P到点A、点B的距离之和最短,
此时x=-
| b |
| 2a |
故P(1,0);
(3)如图所示:抛物线的对称轴为:x=-
| b |
| 2a |
MA2=m2+4,MC2=(3+m)2+1=m2+6m+10,AC2=10;

①若MA=MC,则MA2=MC2,得:
m2+4=m2+6m+10,解得:m=-1,
②若MA=AC,则MA2=AC2,得:
m2+4=10,得:m=±
| 6 |
③若MC=AC,则MC2=AC2,得:
m2+6m+10=10,得:m1=0,m2=-6;
当m=-6时,M、A、C三点共线,构不成三角形,不合题意,故舍去;
综上可知,符合条件的M点,且坐标为 M(1,
| 6 |
| 6 |
看了 如图,已知抛物线y=ax2+...的网友还看了以下:
A市在B市的12km的位置,给B市发货的车以40km/时送货,以60km/时返回A市,往返1时10 2020-04-27 …
在画线处填上恰当的话,使分句前后内容、句式相对应,修辞方法相同。(1)夜晚;白昼。我的祝福装点在星 2020-05-16 …
下列各句中加粗的熟语使用恰当的一句是A.黄金周第一天,峨眉山景区迎来了今年第一场大雪,沸沸扬扬的雪 2020-06-22 …
俄罗斯科学家用含20个质子的钙的一种原子轰击含95个质子的镅原子,结果4次成功合成4个第115号元 2020-07-01 …
四、用“\”画去括号里不恰当的词语。(3分)由于他(化装化妆)成一个商人,日本鬼子没有认出他来。网 2020-07-01 …
下列对于文章内容的说明和分析不恰当的一项是A.丢失项链是偶然事件,但蕴含着必然因素。丢失项链这一情节 2020-11-02 …
关于商鞅变法(1)关于商鞅变法的目的是什么?变法得到了谁的支持?(2)商鞅后来被车裂而死,那么他变法 2020-11-07 …
下列各句中划线词语使用恰当的一项是()(3分)A湖北省面向社会公开招聘副厅级干部,符合条件的人士都可 2020-11-10 …
选择恰当的词语填空。1.在晴天,我们还会遇见一种高积云。这是成群的扁球状的云块,排列得很,云块间露出 2020-12-23 …
下列各句中,加点的成语使用恰当的一项是(3分)A.21世纪的第一个十年已经成为过去。十年,从历史的角 2021-01-19 …