早教吧作业答案频道 -->数学-->
在平面直角坐标系xOy中,抛物线y=-x2+2mx-m2+1的对称轴是直线x=1.(1)求抛物线的表达式;(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;(3)设点M(p,q)为
题目详情
在平面直角坐标系xOy中,抛物线y=-x2+2mx-m2+1的对称轴是直线x=1.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当-1<p<2时,点M关于y轴的对称点都在直线y=kx-4的上方,求k的取值范围.
(1)求抛物线的表达式;
(2)点D(n,y1),E(3,y2)在抛物线上,若y1<y2,请直接写出n的取值范围;
(3)设点M(p,q)为抛物线上的一个动点,当-1<p<2时,点M关于y轴的对称点都在直线y=kx-4的上方,求k的取值范围.
▼优质解答
答案和解析
(1)∵抛物线的对称轴为x=1,
∴x=-
=-
=1.
解得:m=1.
∴抛物线的解析式为y=-x2+2x.
(2)将x=3代入抛物线的解析式得y=-32+2×3=-3.
将y=-3代入得:-x2+2x=-3.
解得:x1=-1,x2=3.
∵a=-1<0,
∴当n<-1或n>3时,y1<y2.
(3)设点M关于y轴对称点为M′,则点M′运动的轨迹如图所示:
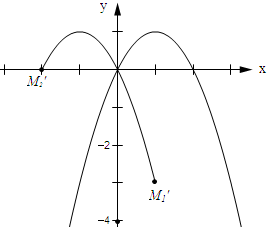
∵当P=-1时,q=-(-1)2+2×(-1)=-3.
∴点M关于y轴的对称点M1′的坐标为(1,-3).
∵当P=2时,q=-22+2×2=0,
∴点M关于y轴的对称点M2′的坐标为(-2,0).
①当k<0时,
∵点M关于y轴的对称点都在直线y=kx-4的上方,
∴-2k-4≤0.
解得:k≥-2.
②当k>0时,
∵点M关于y轴的对称点都在直线y=kx-4的上方,
∴k-4≤-3.
解得;k≤1.
∴k的取值范围是-2≤k≤1.
∴x=-
| b |
| 2a |
| 2m |
| -1×2 |
解得:m=1.
∴抛物线的解析式为y=-x2+2x.
(2)将x=3代入抛物线的解析式得y=-32+2×3=-3.
将y=-3代入得:-x2+2x=-3.
解得:x1=-1,x2=3.
∵a=-1<0,
∴当n<-1或n>3时,y1<y2.
(3)设点M关于y轴对称点为M′,则点M′运动的轨迹如图所示:

∵当P=-1时,q=-(-1)2+2×(-1)=-3.
∴点M关于y轴的对称点M1′的坐标为(1,-3).
∵当P=2时,q=-22+2×2=0,
∴点M关于y轴的对称点M2′的坐标为(-2,0).
①当k<0时,
∵点M关于y轴的对称点都在直线y=kx-4的上方,
∴-2k-4≤0.
解得:k≥-2.
②当k>0时,
∵点M关于y轴的对称点都在直线y=kx-4的上方,
∴k-4≤-3.
解得;k≤1.
∴k的取值范围是-2≤k≤1.
看了 在平面直角坐标系xOy中,抛...的网友还看了以下:
Matlab问题求解.我写了个程序e=0.001;c=[5;4;3;2;1]Q=[5 4 3 2 2020-05-16 …
已知抛物线Y=AX^2+bx+c(a不等于0) 的顶点坐标 为Q(2,-1),且与Y轴交于 点C( 2020-05-16 …
q(n+1)-1+q(n+2)-1=2*qn-2怎么化到q*q+q-2=0 2020-06-12 …
设三次方程x^3+px+q=0三个根互异,且可成等比数列,则公比为可有选项:A-1/2+根3/2i 2020-07-21 …
设某产品的总成本函数和总收入函数分别是C(Q)=3+2√Q,R(Q)=5Q/(Q+1),其中Q是产 2020-07-26 …
平面直角坐标系xoy中,y轴上有一点A(0,1),在x轴上任取一点P,过点P作PA垂线l(1)若l 2020-07-29 …
已知命题P:2+2=5,命题Q:3>2,则下列判断错误的是A.“P∨Q”为真,“┐Q”为假B.“P 2020-08-01 …
关于指数函数和对数函数函数fn(x)=nlog2(x+2),gn(x)=(1/2)^fn(x)(n 2020-08-02 …
设等比数列z1,z2,z3,…,zn,….其中z1=1,z2=a+bi,z3=b+ai(a,b∈R且 2020-10-31 …
求代数式的值:(1)6+2x²-3x+x²+1,其中x=-5(2)4x²+3xy-x²-9,其中x= 2020-12-31 …