设ab是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为{ab}对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤
设 a b 是任意两个不等实数,我们规定:满足不等式 a ≤ x ≤ b 的实数 x 的所有取值的全体叫做闭区间,表示为 {a b} 对于一个函数,如果它的自变量 x 与函数值 y 满足:当 m ≤ x ≤ n 时,有 m ≤ y ≤ n 我们就称此函数是闭区间 {m n} 上的“闭函数” .
( 1 )反比列函数 ![]() 是闭区间 {1 2013} 上的“闭函数”吗?请判断并说明理由;
是闭区间 {1 2013} 上的“闭函数”吗?请判断并说明理由;
( 2 )若一次函数 y=kx+b(k ≠ 0) 是闭区间 {m n} 上的“闭函数”,求此函数的解析式:
1 )是, ![]() 在定义域上是单调递减的,∴当 x ∈ [1 2013] 时, y ∈ {1 2013}
在定义域上是单调递减的,∴当 x ∈ [1 2013] 时, y ∈ {1 2013}
即 ![]() 是闭区间 [1 2013] 上的闭函数
是闭区间 [1 2013] 上的闭函数
( 2 )当 m ≤ x ≤ n ,知 y=kx+b(k ≠ 0) 是单调函数 .
ⅰ)当 k>0 y=kx+b 单调增加,有 mk+b ≤ y ≤ nk+b
∴ ![]()
y=x 满足条件。
ⅱ)当 k<0 , y=kx+b 单调减少,有 nk+b ≤ y ≤ mk+b
∴ ![]()
y=-x+m+n 满足条件 .
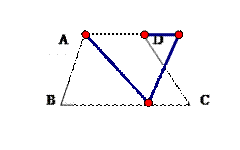
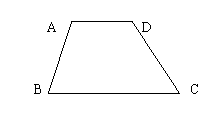
两个全等的RT△ABC和RT△ADC如图所置,点B,A,D在同一直线BI上.在图中做∠CBA的平分 2020-04-26 …
两个全等的Rt△ABC和Rt△EDA如图放置(图5),点B、A、D在同一条直线上.BF是∠ABC的 2020-04-26 …
满足两个条件怎么设公式举例:如何在“绩效考核表”,例如当工作年限是25年,职务岗位是副教授基础绩效 2020-05-17 …
阅读甲、乙两则文字,完成小题(4分)甲哀公问于有若曰:“年饥,用不足,如之何?”有若对曰:“盍彻乎 2020-06-18 …
如图,△ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC=2.现将△ 2020-07-31 …
二元一次方程y=ax∧2+bx+c,表示①至少有一正根②两跟全正③两根全负如何列方程组?(要求用二 2020-08-01 …
在excel中,在同时满足两个条件的情况下返回一个数值,怎么写公式?举例:有全年计划12月计划全年完 2020-11-23 …
汉语--关于“足”与“不足”足可以解释为脚、腿,充足,满足.不足,就只是不充足,不够.把肢体的概念完 2020-11-27 …
如图1,将一张长方形纸片沿对角线剪开,得到两张全等的三角形纸片,如图2,再将这两张三角形纸片摆成如图 2020-12-09 …
Ⅰ、Ⅱ两小题只选一题,如果两题全做,只按Ⅰ题计分.Ⅰ.有机高分子材料、金属材料和无机非金属材料是人类 2020-12-26 …