早教吧作业答案频道 -->数学-->
给出如下四个命题:①回归直线方程必过点;②幂函数y=(m2-m-1)x1-m在R上是减函数;③“a,b∈[0,1]”是“函数有两相异极值点的概率为”的充要条件;④命题“?x∈[1,2],x
题目详情
给出如下四个命题:①回归直线方程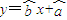 必过点
必过点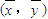 ;②幂函数y=(m 2 -m-1)x 1-m 在R上是减函数;③“a,b∈[0,1]”是“函数
;②幂函数y=(m 2 -m-1)x 1-m 在R上是减函数;③“a,b∈[0,1]”是“函数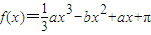 有两相异极值点的概率为
有两相异极值点的概率为 ”的充要条件;④命题“?x∈[1,2],x 2 -1≥0”的否定为“?x∈[1,2],x 2 -1<0”.其中正确命题的个数是( )
”的充要条件;④命题“?x∈[1,2],x 2 -1≥0”的否定为“?x∈[1,2],x 2 -1<0”.其中正确命题的个数是( )
A.①③
B.②③
C.①④
D.②④
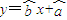 必过点
必过点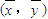 ;②幂函数y=(m 2 -m-1)x 1-m 在R上是减函数;③“a,b∈[0,1]”是“函数
;②幂函数y=(m 2 -m-1)x 1-m 在R上是减函数;③“a,b∈[0,1]”是“函数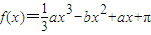 有两相异极值点的概率为
有两相异极值点的概率为 ”的充要条件;④命题“?x∈[1,2],x 2 -1≥0”的否定为“?x∈[1,2],x 2 -1<0”.其中正确命题的个数是( )
”的充要条件;④命题“?x∈[1,2],x 2 -1≥0”的否定为“?x∈[1,2],x 2 -1<0”.其中正确命题的个数是( )A.①③
B.②③
C.①④
D.②④
▼优质解答
答案和解析
分析:
第①个命题说明回归直线通过样本中心点.②:由幂函数的概念判断出m2-m-1等于1;列出等式求出m,再根据象关于y轴对称验证其指数为偶数.再判断其单调性;③:先利用导数求出函数在R上有两个相异极值点的充要条件,得出关于a,b的约束条件,在a-o-b坐标系中画出可行域,再利用几何概型求出两者的面积比即可.④:特称命题“?x∈[1,2],x2-1≥0”的否定是:把?改为?,其它条件不变,然后否定结论,变为一个特称命题.即“?x∈[1,2],x2-1<0”.
对于①,已知n个散点Ai(xi,yi),(i=1,2,3,…,n)的线性回归方程为,若,(其中,),则此回归直线必经过点(),这说明回归直线一定经过样本中心点,故正确.对于②:∵幂函数f(x)=(m2-m-1)x1-m∴m2-m-1=1?m=-1或m=2当m=2时,幂函数f(x)=(m2-m-1)x1-m=x-1,它不在R上是减函数,故错;③:易得f′(x)=ax2-2bx+a,对于函数在R上有两个相异极值点的充要条件:是a≠0且其导函数的判别式大于0,即a≠0且4b2-4a2>0,又若a,b在区间[0,1]上取值,则b>a,点(a,b)满足的区域如图中阴影部分所示,其中正方形区域的面积为1,阴影部分的面积为 ,但反之不能成立,因为当a,b在区间[1,2]上取值时,也得到有两相异极值点的概率为”.故错.对于④,全称命题“?x∈[1,2],x2-1≥0”的否定是特称命题:“?x∈[1,2],x2-1<0”.故正确.故选C.
点评:
本小题主要考查函数单调性的应用、命题的否定、线性回归方程、几何概型等基础知识,考查运算求解能力,考查转化思想.属于基础题.
分析:
第①个命题说明回归直线通过样本中心点.②:由幂函数的概念判断出m2-m-1等于1;列出等式求出m,再根据象关于y轴对称验证其指数为偶数.再判断其单调性;③:先利用导数求出函数在R上有两个相异极值点的充要条件,得出关于a,b的约束条件,在a-o-b坐标系中画出可行域,再利用几何概型求出两者的面积比即可.④:特称命题“?x∈[1,2],x2-1≥0”的否定是:把?改为?,其它条件不变,然后否定结论,变为一个特称命题.即“?x∈[1,2],x2-1<0”.
对于①,已知n个散点Ai(xi,yi),(i=1,2,3,…,n)的线性回归方程为,若,(其中,),则此回归直线必经过点(),这说明回归直线一定经过样本中心点,故正确.对于②:∵幂函数f(x)=(m2-m-1)x1-m∴m2-m-1=1?m=-1或m=2当m=2时,幂函数f(x)=(m2-m-1)x1-m=x-1,它不在R上是减函数,故错;③:易得f′(x)=ax2-2bx+a,对于函数在R上有两个相异极值点的充要条件:是a≠0且其导函数的判别式大于0,即a≠0且4b2-4a2>0,又若a,b在区间[0,1]上取值,则b>a,点(a,b)满足的区域如图中阴影部分所示,其中正方形区域的面积为1,阴影部分的面积为 ,但反之不能成立,因为当a,b在区间[1,2]上取值时,也得到有两相异极值点的概率为”.故错.对于④,全称命题“?x∈[1,2],x2-1≥0”的否定是特称命题:“?x∈[1,2],x2-1<0”.故正确.故选C.
点评:
本小题主要考查函数单调性的应用、命题的否定、线性回归方程、几何概型等基础知识,考查运算求解能力,考查转化思想.属于基础题.
看了 给出如下四个命题:①回归直线...的网友还看了以下:
急:一道物理题,答得好,质量为m的B物体放在质量为M的A物体上面相对静止,以初速度V0冲上倾角为a 2020-05-14 …
题:设m为整数,且4小于m小于40,方程xx-2(2m-3)x+4mm-14m+8=0有两个不相等 2020-05-22 …
超经典的动量守恒问题,快来!物体P,Q质量分别为M,m,且M>m,用弹簧连着处在粗糙的水平面上,他 2020-06-06 …
初学一元二次不等式组 m^2-4≤0 ,m≤0,16(m-2)^2-16<0,怎么参考书最后答案是 2020-06-27 …
关于握手问题m是偶数1)若干个人都相互握手一次,每个人的握手次数之和为m2)若干个人都相互握手一次 2020-07-30 …
下列命题中正确的是()①“若x2+y2≠0,则x,y不全为零”的否命题.②“正多边形都相似”的逆命 2020-08-01 …
不正确的命题(1816:26:49)1、平面A外两条直线m和n在平面内A的射影分别为m’和n’,给出 2020-11-14 …
高一物理动量问题总质量为M的火箭以速度V0飞行,质量为m的燃料相对于火箭以速度u向后喷出,则火箭的速 2020-12-15 …
化学选择填充题已知正价元素A与氧元素组成的氧化物的相对分子质量为M,它与Cl元素组成的化合物的相对分 2021-01-13 …
3个互不相等的有理数,它们既可以表示为1,M+N,M的形式,又可以表示为M/N,0,N的形式,求这个 2021-02-02 …