早教吧作业答案频道 -->数学-->
回顾我们学习了三角形的全等,知道了判定两个三角形全等的基本事实有“SAS”、“ASA”、“SSS”,以及由基本事实得到的推论“AAS,我们还得到一个定理“HL”,下面对“两个三角形
题目详情
【回顾】我们学习了三角形的全等,知道了判定两个三角形全等的基本事实有“SAS”、“ASA”、“SSS”,以及由基本事实得到的推论“AAS,我们还得到一个定理“HL”,下面对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
【思考】
我们将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【探究】
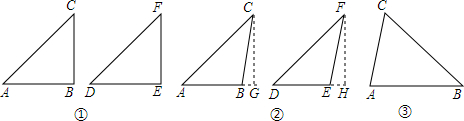
(1)第一种情况:当∠B是直角时,△ABC与DEF.是否全等?___,如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据___,可以知道___.
(2)第二种情况:当∠B是钝角时,△ABC≌△DEF.如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC,∠DEF都是钝角,求证:△ABC≌△DEF(请你继续完成证明过程).
证明:如图,过C作CG⊥AB交AB的延长线于点G,过F作FH⊥DE交DE的延长线于点H,
(3)第三种情况:当∠B是锐角时,即在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角.△ABC和△DEF是否全等,请你用尺规在图③中作出△DEF,直接写出你的结论.
(不写作法,保留作图痕迹)
【思考】
我们将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.
【探究】

(1)第一种情况:当∠B是直角时,△ABC与DEF.是否全等?___,如图①,在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据___,可以知道___.
(2)第二种情况:当∠B是钝角时,△ABC≌△DEF.如图②,在△ABC和△DEF中,AC=DF,BC=EF,∠ABC=∠DEF,且∠ABC,∠DEF都是钝角,求证:△ABC≌△DEF(请你继续完成证明过程).
证明:如图,过C作CG⊥AB交AB的延长线于点G,过F作FH⊥DE交DE的延长线于点H,
(3)第三种情况:当∠B是锐角时,即在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B,∠E都是锐角.△ABC和△DEF是否全等,请你用尺规在图③中作出△DEF,直接写出你的结论.
(不写作法,保留作图痕迹)
▼优质解答
答案和解析
(1)答:全等;在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E=90°,根据“HL“,可以知道Rt△ABC≌Rt△DEF;
故答案为:全等,HL,Rt△ABC≌Rt△DEF;
(2)证明:∵∠B=∠E,
∴180°-∠B=180°-∠E,
即∠CBG=∠FEH,
在△CBG和△FEH中,
,
∴△CBG≌△FEH(AAS),
∴CG=FH,
在Rt△ACG和Rt△DFH中,
,
∴Rt△ACG≌Rt△DFH(HL),
∴∠A=∠D,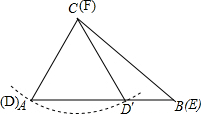
在△ABC和△DEF中,
,
∴△ABC≌△DEF(AAS).
(3)第三种情况:如图所示:
以C为圆心,AC长为半径画弧,交AB于D;
则DF=AC,△DEF≌△ABC,△D′EF和△ABC不全等.
故答案为:全等,HL,Rt△ABC≌Rt△DEF;
(2)证明:∵∠B=∠E,
∴180°-∠B=180°-∠E,
即∠CBG=∠FEH,
在△CBG和△FEH中,
|
∴△CBG≌△FEH(AAS),
∴CG=FH,
在Rt△ACG和Rt△DFH中,
|
∴Rt△ACG≌Rt△DFH(HL),
∴∠A=∠D,

在△ABC和△DEF中,
|
∴△ABC≌△DEF(AAS).
(3)第三种情况:如图所示:
以C为圆心,AC长为半径画弧,交AB于D;
则DF=AC,△DEF≌△ABC,△D′EF和△ABC不全等.
看了 回顾我们学习了三角形的全等,...的网友还看了以下:
(1)下面的说法错误的是:(a)圆只有一个对称中心(b)等边三角形有三个对称中心(c)正方形有一个 2020-04-11 …
数一数有个三角形有个平行四边形有个梯形. 2020-04-25 …
第一个图形一共有1个长方形,第2个图形有5个长方形,第3个图形有11个长方形,则10个图形有()个 2020-06-19 …
在小说《祝福》、《荷花淀》、《边城》中,分别塑造了祥林嫂、水生嫂、翠翠三个女性形象,她们各有个性, 2020-06-29 …
在图中,按照柱、锥、球分类,属于柱体一类的有个图形;按照组成来分类,组成它们的面中至少有一个是曲的 2020-07-05 …
如图,每个小方格都是边长为1的正方形.(1)图中面积为2的长方形有个(2)图中长方形(包括正方形) 2020-07-20 …
将一些半径相同的小圆按如图所示的规律摆放:第1个图形有6个小圆,第2个图形有10个小圆,第3个图形 2020-07-29 …
给出一个凸10边形及其所有对角线,在以该凸10边形的顶点及所有对角线的交点为顶点的三角形中,至少有 2020-08-02 …
如图是半个正方形,它被分成一个一个小的等腰三角形,图中,正方形有个,三角形有个. 2020-08-03 …
边长为整数且周长为24的三角形有个其中不等边三角形有个等腰三角形有个直角三角形有个 2020-08-03 …