早教吧作业答案频道 -->数学-->
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.(1)求证:OD∥平面PAB;(2)当k=12时,求直线PA与平面PBC所成角的正弦值;(3)当k为何值时,O在平面PBC内
题目详情
如图,在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点,OP⊥平面ABC.
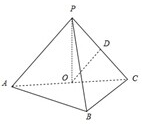
(1)求证:OD∥平面PAB;
(2)当k=
时,求直线PA与平面PBC所成角的正弦值;
(3)当k为何值时,O在平面PBC内的射影恰好为△PBC的重心.

(1)求证:OD∥平面PAB;
(2)当k=
| 1 |
| 2 |
(3)当k为何值时,O在平面PBC内的射影恰好为△PBC的重心.
▼优质解答
答案和解析
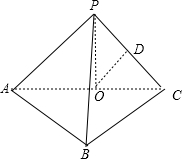 (Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点
(Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点
∴OD∥AP
∵AP⊂平面PAB,OD⊄平面PAB
∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC OA=OC
∴OA=OB=OC
又∵OP⊥平面ABC
∴PA=PB=PC
取BC的中点E,连结PE,
则:BC⊥平面POE
作OF⊥PE于F,连结DF,
则:OF⊥平面PBC
∴∠ODF是DO与平面PBC所成的角.
由OD∥PA
∴∠ODF是PA与平面PBC所成的角
在Rt△ODF中,sin∠ODF=
=
PA与平面PBC所成的角为:arcsin
;
(Ⅲ)由(Ⅱ)知:OF⊥平面PBC
∴F是O在平面PBC内的射影.
∵D是PC的中点,
若点F是△PBC的重心,
则:B、F、D三点共线.
所以,直线OB在平面PBC内的射影为直线BD.
∵OB⊥PC
PC⊥BD
∴PB=BC
即:k=1
反之,当k=1时,三棱锥O-PBC为正三棱锥.
O在平面PBC内的射影恰好为△PBC的重心
 (Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点
(Ⅰ)证明:在三棱锥P-ABC中,AB⊥BC,AB=BC=kPA,点O、D分别是AC、PC的中点∴OD∥AP
∵AP⊂平面PAB,OD⊄平面PAB
∴OD∥平面PAB.
(Ⅱ)∵AB⊥BC OA=OC
∴OA=OB=OC
又∵OP⊥平面ABC
∴PA=PB=PC
取BC的中点E,连结PE,
则:BC⊥平面POE
作OF⊥PE于F,连结DF,
则:OF⊥平面PBC
∴∠ODF是DO与平面PBC所成的角.
由OD∥PA
∴∠ODF是PA与平面PBC所成的角
在Rt△ODF中,sin∠ODF=
| OF |
| OD |
| ||
| 30 |
PA与平面PBC所成的角为:arcsin
| ||
| 30 |
(Ⅲ)由(Ⅱ)知:OF⊥平面PBC
∴F是O在平面PBC内的射影.
∵D是PC的中点,
若点F是△PBC的重心,
则:B、F、D三点共线.
所以,直线OB在平面PBC内的射影为直线BD.
∵OB⊥PC
PC⊥BD
∴PB=BC
即:k=1
反之,当k=1时,三棱锥O-PBC为正三棱锥.
O在平面PBC内的射影恰好为△PBC的重心
看了 如图,在三棱锥P-ABC中,...的网友还看了以下:
已知复数W=1i,Z=ai(a属于R)复数W-Z,WZ在复平面内对应的点分别为A,B,O为坐标已知 2020-06-14 …
根式计算化简1、(1/x^2-3x+2)+(1/x^2-x)+(1/x^2+x)+(1/x^2+3 2020-07-30 …
正余弦定理运用一题在等边三角形ABC中,AB=a,O为等边三角形的中心,过O的直线交AB于M,交A 2020-08-02 …
(j010•南通模拟)作为对数运算法则:lg(o+b)=lgo+lgb(o>0,b>0)是不正确的. 2020-11-12 …
1.若集合A={x|(a-1)x^2+2x+1=o}中只含有一个元素,求实数a2.已知集合A={1, 2020-12-07 …
归纳:(一)在数轴上,点A表示数-3,点O表示原点,求点A、O之间的距离;根据绝对值的定义:一个数所 2020-12-07 …
如下图所示为一弹簧振子,设向右为正方向,振子的运动()A.C→O时,位移是正值,速度是正值B.O→B 2020-12-31 …
两条河M,N,在点O汇合,∠MON=45,形成一个半岛,上面有一个古迹a.现计划,在两条河上个修建一 2021-01-13 …
某同学做“互成角度两个力的合成”的实验时得到如图所示的图(F与A、O共线),其中A为固定橡皮条的图钉 2021-01-15 …
在验证“互成角度的两个力的合成”的实验中,某小组的出如图所示的图(F与A、O共线),其中A为固定橡皮 2021-01-15 …