在三棱锥P-ABC中，平面PAC⊥平面ABC，AB⊥BC，若△PAC为正三角形且边长为2，则三棱锥P-ABC外接球的体积为（）A.πB.32327πC.34πD.3227π

Question

在三棱锥P-ABC中，平面PAC⊥平面ABC，AB⊥BC，若△PAC为正三角形且边长为2，则三棱锥P-ABC外接球的体积为（　　）

A. π

B.

(32√(3))/(27)π

C.

(3)/(4)π

D.

(32)/(27)π

Answer 1

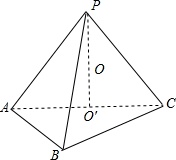取AC的中点O′，则PO′⊥AC，PO′=√(3)
∵AB⊥BC，
∴AC为△ABC外接圆的直径，
∴球心O在PO′上，
设球的半径为R，则R²=1²+（√(3)-R）²，
∴R=(2)/(√(3))，
∴三棱锥P-ABC外接球的体积为(4)/(3)πR3=(4)/(3)π•((2)/(√(3)))3=(32√(3))/(27)π．
故选：B．