早教吧作业答案频道 -->数学-->
如图所示,已知四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC的中点.(1)指出平面ADM与PB的交点N所在位置,并给出理由;(2)求平面ADM将四棱锥P-ABCD分成上下两部分的
题目详情
如图所示,已知四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,PA=BC=1,AB=2,M为PC的中点.
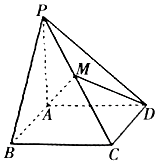
(1)指出平面ADM与PB的交点N所在位置,并给出理由;
(2)求平面ADM将四棱锥P-ABCD分成上下两部分的体积比.

(1)指出平面ADM与PB的交点N所在位置,并给出理由;
(2)求平面ADM将四棱锥P-ABCD分成上下两部分的体积比.
▼优质解答
答案和解析
(1)N为PB中点.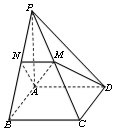
理由如下:
∵AD∥BC,AD⊄平面PBC,BC⊂平面PBC,
∴AD∥平面PBC,
又∵AD⊂平面AMD,平面AMD∩平面PBC=MN,
∴AD∥MN,
又∵M为PC的中点,∴N为PB的中点.
(2)∵PA⊥底面ABCD,∴AD⊥PA
又∵底面ABCD为矩形,∴AD⊥AB
∵PA∩AB=A,∴AD⊥平面PAB,又∵AN⊂平面PAB,∴AD⊥AN,
∵MN是△PBC的中位线,且BC=1,∴MN=
,
又AN=
=
,∴SADMN=
×(
+1)×
=
,
∵P点到截面ADMN的距离为P到直线AN的距离d=
,
∴四棱锥P-ADMN的体积V1=
×
×
=
而四棱锥P-ABCD的体积V=
×2×1=
,
∴四棱锥被截下部分体积V2=V-V1=
-
=
故上、下两部分体积比

理由如下:
∵AD∥BC,AD⊄平面PBC,BC⊂平面PBC,
∴AD∥平面PBC,
又∵AD⊂平面AMD,平面AMD∩平面PBC=MN,
∴AD∥MN,
又∵M为PC的中点,∴N为PB的中点.
(2)∵PA⊥底面ABCD,∴AD⊥PA
又∵底面ABCD为矩形,∴AD⊥AB
∵PA∩AB=A,∴AD⊥平面PAB,又∵AN⊂平面PAB,∴AD⊥AN,
∵MN是△PBC的中位线,且BC=1,∴MN=
| 1 |
| 2 |
又AN=
| PB |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
3
| ||
| 8 |
∵P点到截面ADMN的距离为P到直线AN的距离d=
| 2 | ||
|
∴四棱锥P-ADMN的体积V1=
| 1 |
| 3 |
3
| ||
| 8 |
| 2 | ||
|
| 1 |
| 4 |
而四棱锥P-ABCD的体积V=
| 1 |
| 3 |
| 2 |
| 3 |
∴四棱锥被截下部分体积V2=V-V1=
| 2 |
| 3 |
| 1 |
| 4 |
| 5 |
| 12 |
故上、下两部分体积比
| V1 |
| V2 |
看了 如图所示,已知四棱锥P-AB...的网友还看了以下:
点A是函数y=2/x(x>0)图像上任意一点(一象限),过A点分别作x、y的平行线交函数y=1/x 2020-04-05 …
在一个大正方体中截去一个小正方体,在()上截表面积最大A.顶点B.面C.棱最好写出为什么 2020-04-09 …
三道二次函数,请写下具体过程14.已知二次函数y=ax^2+bx+c的图象经过P(1,2)和点Q( 2020-05-13 …
比中交下列每组字母或单词的读音,相同的用S,不同的用D表示:b,d,c,e,c,a,b,c,a,e 2020-05-14 …
A地海拔高度是-40m,B地比A地高20m,C地又比B地高30m,试用正数或负数表示B、C两地的海 2020-05-16 …
正数与负数的习题之二感兴趣就来做咯A地海拔高度是-40M,B地比A地高20m,C地又比B地高30m 2020-05-16 …
向无隶属关系的有关主管部门请求批准,用( ):A.请示B.函C.报告D.通知 2020-05-31 …
如图所示,在点电荷形成的电场中有a、b、c三点,它们到点电荷的距离分别为ra、rb和rc,且rb- 2020-06-12 …
已知△ABC的三个内角A,B,C所对的边分别为a,b,c,若b-a=c-b=1且C=2A,求cos 2020-07-18 …
如图,在菱形ABCD内作一个等边△AEF,AE=AB.(1)∠BAE与∠DAF是否相等?请说明理由 2020-07-30 …
 扫描下载二维码
扫描下载二维码
