早教吧作业答案频道 -->数学-->
已知边长为a的正方形ABCD外有一点P,且PA⊥平面ABCD,PA=a,求二面角B-PA-C和P-BC-A的大小.
题目详情
已知边长为a的正方形ABCD外有一点P,且PA⊥平面ABCD,PA=a,求二面角B-PA-C和P-BC-A的大小.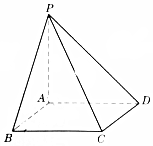

▼优质解答
答案和解析
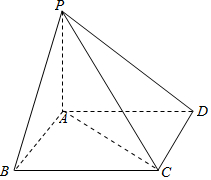 ∵边长为a的正方形ABCD外有一点P,∵PA⊥AB,PA=AB,∴∠PBA=45°,
∵边长为a的正方形ABCD外有一点P,∵PA⊥AB,PA=AB,∴∠PBA=45°,
连接AC,PA⊥平面ABCD,可得AB⊥PA,
PA⊥AC,二面角B-PA-C即为∠BAC即为所求的角,为45°.
∵边长为a的正方形ABCD外有一点P,且PA⊥平面ABCD,
PA=a,又∵ABCD为正方形,∴AB⊥BC,
∵PA∩AB=A,∴BC⊥平面PAB,
∵PA⊂平面PAB,∴BC⊥PA,
又CD⊥BC,
∴二面角P-BC-A的平面角即为∠PBA即为所求的角,为45°.
二面角B-PA-C和P-BC-A的大小都是45°.
 ∵边长为a的正方形ABCD外有一点P,∵PA⊥AB,PA=AB,∴∠PBA=45°,
∵边长为a的正方形ABCD外有一点P,∵PA⊥AB,PA=AB,∴∠PBA=45°,连接AC,PA⊥平面ABCD,可得AB⊥PA,
PA⊥AC,二面角B-PA-C即为∠BAC即为所求的角,为45°.
∵边长为a的正方形ABCD外有一点P,且PA⊥平面ABCD,
PA=a,又∵ABCD为正方形,∴AB⊥BC,
∵PA∩AB=A,∴BC⊥平面PAB,
∵PA⊂平面PAB,∴BC⊥PA,
又CD⊥BC,
∴二面角P-BC-A的平面角即为∠PBA即为所求的角,为45°.
二面角B-PA-C和P-BC-A的大小都是45°.
看了 已知边长为a的正方形ABCD...的网友还看了以下:
求过点P且垂直于直线l的直线的方程P(4,-3)L:X=3 2020-05-17 …
求过点P且垂直于直线l的直线的方程P(-2,3),ly=3x-1 2020-05-22 …
急求~~1,在三角形ABC中,a平方+b平方+c平方sinC=2倍根号三乘absinC,判i断三角 2020-07-14 …
关于概率的问题P(W|C)的求解如下:P(W|C)=P(W)P(C|W)/P(C)其中,P(C)是 2020-07-30 …
1.已知A={(x,y)|y/1-x平方=1},B={(x,y)|y=1-x平方},C={(x,y 2020-08-01 …
X、Y分别服从参数为(n,p)(m,p)的二项分布,通过计算求出X+Y的分布我用的方法Z=X+YP( 2020-10-31 …
有两条式子:若x1,x2是一元二次方程ax的平方+bx+c=0(a不等于0)的两根,则x1+x2=- 2020-11-07 …
(1)已知关于Ⅹ的方程Ⅹ²+pⅩ+q=0的两个根是1和-3,求p,q的值?(2)当Ⅹ为何值时,代数式 2020-11-11 …
在RT三角形ABC中,角C=90°,若a=s的方减t的方,c=s的方加t的方(s>t>0),则b=? 2020-12-02 …
试说明关于x的方程(p²-6p+20)x²+2px-108=0,不论p取何值时,该方程都是一元二次方 2020-12-23 …