如图所示，水平转台上有一个质量为m的物块，用长为L的细绳将物块连接在转轴上，细线与竖直转轴的夹角为θ角，此时绳中张力为零，物块与转台间动摩擦因数为μ（μ<tanθ），最大静摩

Question

如图所示，水平转台上有一个质量为m的物块，用长为L的细绳将物块连接在转轴上，细线与竖直转轴的夹角为θ角，此时绳中张力为零，物块与转台间动摩擦因数为μ（μ<tanθ），最大静摩擦力等于滑动摩擦力，物块随转台由静止开始缓慢加速转动，则下列说法中正确的是（　　）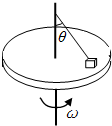

A. 当转台的ω=

√((μg)/(2Lsinθ))时，物块受到四个力作用

B. 当转台的ω=

√((μg)/(Lsinθ))时，细绳恰好产生拉力

C. 当转台的ω=

√((2g)/(3Lcosθ))时，物块恰好对转台无压力

D. 当转台的ω=

√((g)/(Lcosθ))时，转台对物块做的功为(mgLsin2θ)/(2cosθ)

Answer 1

A、当转台的角速度比较小时，物块只受重力、支持力和摩擦力，当细绳恰好要产生拉力时：
μmg=m

ω

2 1

(Lsinθ)，
解得：ω1=√((μg)/(Lsinθ))，由于√((μg)/(2Lsinθ))<ω1=√((μg)/(Lsinθ))，所以当ω=ω1=√((μg)/(Lsinθ))时，细线中张力为零，即ω=√((μg)/(2Lsinθ))，物块只受到重力、支持力和摩擦力的作用．故A错误，B正确，C错误；
D、随速度的增大，细绳上的拉力增大，当物块恰好要离开转台时，物块受到重力和细绳的拉力的作用，则：
mgtanθ=m

ω

2 2

(Lsinθ)
解得：ω2=√((g)/(Lcosθ))，
当ω=√((g)/(Lcosθ))时，小球恰好要离开转台，转台对物块做的功转化为物块的动能，所以：W=(1)/(2)mv2=(1)/(2)m(ω2•Lsinθ)2=(mgLsin2θ)/(2cosθ)．故D正确．
故选：BD