早教吧作业答案频道 -->数学-->
△ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.(1)如图1,若∠ACB=90°,求证:BF+CE=BC;(2)如图2,若∠ABC与∠ACB是任意角度,(1)中的结论是否仍成立?请说明你
题目详情
△ABC中,∠A=60°,BE,CF分别是∠ABC和∠ACB的平分线,CF与BE相交于点O.
(1)如图1,若∠ACB=90°,求证:BF+CE=BC;
(2)如图2,若∠ABC与∠ACB是任意角度,(1)中的结论是否仍成立?请说明你的理由.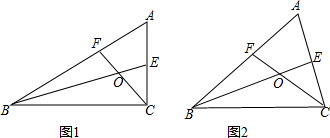
(1)如图1,若∠ACB=90°,求证:BF+CE=BC;
(2)如图2,若∠ABC与∠ACB是任意角度,(1)中的结论是否仍成立?请说明你的理由.

▼优质解答
答案和解析
(1)证明:如图1中,在CB上截取CM=CE,连接OM.
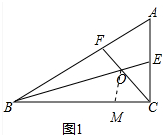
∵∠A=60°,∠ACB=90°,
又∵BE,CF分别是∠ABC和∠ACB的平分线,
∴∠FCA=∠FCB=45°,∠ABE=∠EBC=15°,
∴∠BFC=∠A+∠ACF=105°,∠CEB=∠A+∠ABE=75°
在△OCE和△OCM中,
,
∴△OCE≌△OCM,
∴∠CEO=∠OEC=75°,
∴∠BMO=180°-∠CMO=105°,
∴∠BFO=∠BMO,
在△OBF或△OBM中,
,
∴△OBF≌△OBM,
∴BF=BM,
∴BC=BM+CM=BF+CE.
(2)结论:成立,BC=BF+CE.
理由:如图2中,在CB上截取CM=CE,连接OM.
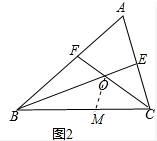
∵∠A=60°,
∴
∠ABC+
∠ACB=60°,
即∠ABE+∠ACF=60°,
∵∠BFO=∠A+∠FCA,∠CEO=∠A+∠ABE,
∴∠BFO+∠CEO=2∠A+∠FCA+∠ABE=180°,
由△OCM≌△OCE,得∠CEO=∠CMO,
∵∠CMO+∠BMO=180°,
∴∠BFO=∠BMO,
在△OBF或△OBM中,
,
∴△OBF≌△OBM,
∴BF=BM,
∴BC=BM+CM=BF+CE.

∵∠A=60°,∠ACB=90°,
又∵BE,CF分别是∠ABC和∠ACB的平分线,
∴∠FCA=∠FCB=45°,∠ABE=∠EBC=15°,
∴∠BFC=∠A+∠ACF=105°,∠CEB=∠A+∠ABE=75°
在△OCE和△OCM中,
|
∴△OCE≌△OCM,
∴∠CEO=∠OEC=75°,
∴∠BMO=180°-∠CMO=105°,
∴∠BFO=∠BMO,
在△OBF或△OBM中,
|
∴△OBF≌△OBM,
∴BF=BM,
∴BC=BM+CM=BF+CE.
(2)结论:成立,BC=BF+CE.
理由:如图2中,在CB上截取CM=CE,连接OM.

∵∠A=60°,
∴
| 1 |
| 2 |
| 1 |
| 2 |
即∠ABE+∠ACF=60°,
∵∠BFO=∠A+∠FCA,∠CEO=∠A+∠ABE,
∴∠BFO+∠CEO=2∠A+∠FCA+∠ABE=180°,
由△OCM≌△OCE,得∠CEO=∠CMO,
∵∠CMO+∠BMO=180°,
∴∠BFO=∠BMO,
在△OBF或△OBM中,
|
∴△OBF≌△OBM,
∴BF=BM,
∴BC=BM+CM=BF+CE.
看了 △ABC中,∠A=60°,B...的网友还看了以下:
1.判断a、b、c能否构成三角形的三条边长的条件是().选项:a、a>0&&b>0&&c>0b、a+ 2020-03-31 …
任务说明:输入三角形的三条边a,b,c,判断它们能否构成三角形.若能构成三角形,指出是何种三角形. 2020-04-06 …
一道关于VF的题题目是这样的:从键盘输入a、b、c的值,判断它们能否构成三角形的三条边.如果能构成 2020-05-13 …
a,b,c是直角三角形的三条边,c是斜边.以1\a,1\b,1\c的长为边的三条线段能否组成直角三 2020-05-14 …
判断此命题是否正确A,B,C为三角形的三个角,若sinAsinBsinC>cosAcosBcosC 2020-05-20 …
已知a,b,c满足la一根号8l十根号b一5十(c一3的根号2)2=0.(1)求a,b,c的值;2 2020-06-06 …
11.判断是否能构成三角形定义三个字节的正数(A、B、C),判断是否能构成三角形,如能,则显示“Y 2020-07-22 …
若a、b、c为直角三角形的三条边,斜边c上的高为h.1)以a+b、c+h和h的长为边能否组成直角三 2020-08-02 …
可否构成直角三角形?在△ABC中,∠C=90°,D是AB的中点,E、F分别在AC和BC上,且DE⊥D 2020-11-03 …
已知在三角形ABC中,角C大于角B,AD垂直BC于D,AE评分角BAC.1求证角EAD=二分之一(角 2020-12-09 …