早教吧作业答案频道 -->数学-->
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.(1)求证:GE是⊙O的切线;(2)若tanC=13,
题目详情
如图,AB为⊙O直径,C是⊙O上一点,CO⊥AB于点O,弦CD与AB交于点F,过点D作∠CDE=∠DFE,DE交AB的延长线于点E,过点A作⊙O的切线交ED的延长线于点G.
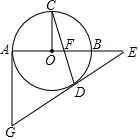
(1)求证:GE是⊙O的切线;
(2)若tanC=
,BE=4,求AG的长.

(1)求证:GE是⊙O的切线;
(2)若tanC=
| 1 |
| 3 |
▼优质解答
答案和解析
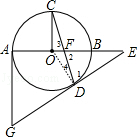 (1)证明:连接OD,如图,
(1)证明:连接OD,如图,
∵∠1=∠2,
而∠2=∠3,
∴∠3=∠1,
∵OC⊥AB,
∴∠3+∠C=90°,
∴∠1+∠C=90°,
而OC=OD,
∴∠C=∠4,
∴∠1+∠4=90°,即∠ODE=90°,
∴OD⊥DE,
∴GE是⊙O的切线;
(2) 设OF=x,则OC=3x,
∴BF=2x,
∵∠1=∠2,
∴ED=EF=2x+4,
在Rt△ODE中,
∵OD2+DE2=OE2,
∴(3x)2+(2x+4)2=(4+3x)2,解得x=2,
∴OD=6,DE=8,OE=10
又∵△AGE∽△DOE,
AE=16,
可得AG=12.
 (1)证明:连接OD,如图,
(1)证明:连接OD,如图,∵∠1=∠2,
而∠2=∠3,
∴∠3=∠1,
∵OC⊥AB,
∴∠3+∠C=90°,
∴∠1+∠C=90°,
而OC=OD,
∴∠C=∠4,
∴∠1+∠4=90°,即∠ODE=90°,
∴OD⊥DE,
∴GE是⊙O的切线;
(2) 设OF=x,则OC=3x,
∴BF=2x,
∵∠1=∠2,
∴ED=EF=2x+4,
在Rt△ODE中,
∵OD2+DE2=OE2,
∴(3x)2+(2x+4)2=(4+3x)2,解得x=2,
∴OD=6,DE=8,OE=10
又∵△AGE∽△DOE,
AE=16,
可得AG=12.
看了 如图,AB为⊙O直径,C是⊙...的网友还看了以下:
已知A与(B或C)=D,能否得出结论:Aand非(B与C)=非D?已知定理:A与(B或C)=D如: 2020-04-06 …
将25克A、5克B和10克C一并充入容积为10L的密闭容器中,加热发生反应.2分钟后分析混合物中含 2020-04-26 …
现有A,B,C,D四种物质,已知A,B为黑色粉末,C,D为无色气体,A,B在高温下作用能生成D,A 2020-05-17 …
#includemain(){inta=0x7fffffff,b=025;floatf1=123. 2020-05-19 …
测控系统中所采用的高质量的D/A转换器,其非线性误差通常在( )误差范围之内。A.±1LSBB.±2 2020-05-24 …
一个微机系统通过其D/A接口对被控模拟量实行控制,则该系统的控制精度取决于所使用的 D/A转换器的 2020-05-24 …
A.πA,D(σC=D(R×S))B.πA,R,D(σS,C=R,D/(R×S))C.πA,R,D( 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σR.C=S.D(R×S))C.πA,R.D(σ 2020-05-26 …
A.πA,D(σC=D(R×S))B.πA,R.D(σS.C=R.D(R×S))C.πA,R.D(σ 2020-05-26 …
matlab中怎么计算x='-(a^2*c-b*d^2-a^2*e+c*d^2-2*a*c*d+2 2020-07-24 …