如图，过O外一点P作O的两条切线，切点分别为A、B，点M是劣弧AB上的任一点，过M作0的切线分别交PA、PB于点C、D，过圆心O且垂直于OP的直线与PA、PB分别交于点E、F，那么EC•FDEF2的值为（

Question

如图，过 O外一点P作 O的两条切线，切点分别为A、B，点M是劣弧

AB

上的任一点，过M作 0的切线分别交PA、PB于点C、D，过圆心O且垂直于OP的直线与PA、PB分别交于点E、F，那么(EC•FD)/(EF2)的值为（　　）

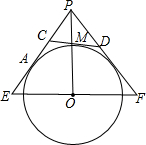
A.

(1)/(4)

B.

(1)/(2)

C. 1

D. 2

Answer 1

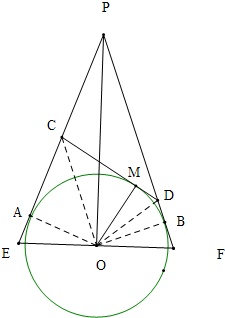∵PA、PB、CD都是 O的切线，
∴∠OPE=∠OPF，∠OAC=∠OCD，∠ODM=∠ODB，OA⊥PE，OM⊥D，OB⊥PF，
∴∠OAC=∠OMC=∠OMD=∠OBD=90°，
∵∠COA+∠AOC=90°，∠OCD+∠COM=90°∴∠COA=∠COM，
同理∠DOM=∠DOB，
∵PO⊥EF，
∴∠OPE=∠POF=90°，
∴∠OPE+∠E=90°，∠OPF+∠F=90°，
∴∠E=∠F，
∴PE=PF，∵∠EPO=∠FPO，
∴OE=OF，
∵∠E+∠AOE=90°，∠F+∠FOB=90°，
∴∠AOE=∠BOF，
∵∠AOE+∠AOC+∠COD+∠MOD+∠DOB+∠FOB=180°，
∴2∠BOF+2∠AOC+2∠DOB=180°，
∴∠BOF+∠AOC+∠DOB=90°，
∴∠AOC+∠DOF=90°，∵∠AOC+∠ACO=90°，
∴∠ACO=∠DOF，∵∠E=∠F，
∴△EOC∽△FDO，
∴(EO)/(DF)=(EC)/(FO)，
∴EC•DF=OE•OF=OE²，
∴(EC•DF)/(EF2)=(OE2)/(4OE2)=(1)/(4)．
故选A．