早教吧作业答案频道 -->数学-->
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO.(1)求证PO⊥AC;(2)求异面直线PA与OE所成角的大小.
题目详情
如图,圆锥的底面圆心为O,直径为AB,C为半圆弧AB的中点,E为劣弧CB的中点,且AB=2PO.
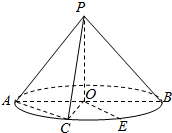
(1)求证PO⊥AC;
(2)求异面直线PA与OE所成角的大小.

(1)求证PO⊥AC;
(2)求异面直线PA与OE所成角的大小.
▼优质解答
答案和解析
(1)证明:∵PO是圆锥的高,
∴PO⊥底面圆O,
又AC∈底面圆O,
∴PO⊥AC.
(2) ∵C为半圆弧AB的中点,∴∠AOC=90°=∠BOC,
∴∠BAC=45°,
又∵E为劣弧CB的中点,
∴∠BOE=45°=∠BAC,∴OE∥AC,
∴异面直线PA与OE所成角即为∠PAC,
∵AB=2PO,又直径AB=2AO,∴PO=AO,
∵PO⊥底面圆O,∴PO⊥OC,即∠POC=90°=∠AOC,
∴△AOC≌△POC,∴AC=PC,
又∵圆锥母线PA=PC,∴△PAC为正三角形,
∴∠PAC=60°,
∴异面直线PA与OE所成角的大小为60°.
∴PO⊥底面圆O,
又AC∈底面圆O,
∴PO⊥AC.

(2) ∵C为半圆弧AB的中点,∴∠AOC=90°=∠BOC,
∴∠BAC=45°,
又∵E为劣弧CB的中点,
∴∠BOE=45°=∠BAC,∴OE∥AC,
∴异面直线PA与OE所成角即为∠PAC,
∵AB=2PO,又直径AB=2AO,∴PO=AO,
∵PO⊥底面圆O,∴PO⊥OC,即∠POC=90°=∠AOC,
∴△AOC≌△POC,∴AC=PC,
又∵圆锥母线PA=PC,∴△PAC为正三角形,
∴∠PAC=60°,
∴异面直线PA与OE所成角的大小为60°.
看了 如图,圆锥的底面圆心为O,直...的网友还看了以下:
AA、B、C、D、E、F六种短周期元素,原子序数依次增大.A、E同主族,且E元素原子的核外电子数是 2020-04-08 …
若只通过测定装置中C、D的增重来确定x,则装置按气流方向接口的连接顺序为()A.a→b→c→eB. 2020-05-17 …
如图中的A-F所表示物质均为初中化学常见的纯净物.其中A、C、B的相对分子质量依次增加1,且均含有 2020-06-24 …
有A、B、C、D、E、F、G七种元素,除E为第四周期元素外其余均为短周期元素.A、E、G位于元素周 2020-07-08 …
在学习了元素化合物知识后,小丽构建了以下知识网络,并对它进行了推理和判断.A~E是初中化学常见的五种 2020-11-01 …
已知向量a≠e,|e|=1,对任意t∈R,恒有|a-te|≥|a-e|,则[]A.a⊥eB.a⊥(a 2020-11-02 …
某二倍体植物的开花时间有正常开花、早花和晚花三种表现,由促进和抑制两类基因控制.基因A促进开花,基因 2020-11-08 …
(2014•开封二模)输入a=ln0.8,b=e12,c=2-e,经过下列程序运算后,输出a,b的值 2020-11-12 …
A、B、C、D为四种原子序数依次增大的短周期元素,E为第四周期副族元素.A、E最外层电子排布式均为n 2020-12-05 …
读图,完成28~29题.图中的地质作用属于内力作用的是()A.a、c、dB.a、e、fC.c、d、e 2020-12-28 …