早教吧作业答案频道 -->物理-->
如图所示,光滑水平面上有一质量为2M、半径为R(R足够大)的圆弧曲面C,质量为M的小球B置于其底端,另一个小球A质量为M2,以v0=6m/s的速度向B运动,并与B发生弹性碰撞,不计一切摩擦,小
题目详情
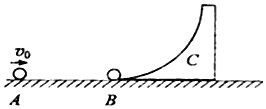
如图所示,光滑水平面上有一质量为2M、半径为R(R足够大)的圆弧曲面C,质量为M的小球B置于其底端,另一个小球A质量为
,以v0=6m/s的速度向B运动,并与B发生弹性碰撞,不计一切摩擦,小球均视为质点,求:
(1)小球B的最大速率;
(2)小球B运动到圆弧曲面最高点时的速率;
(3)通过计算判断小球B能否与小球A再次发生碰撞.
| M |
| 2 |

(1)小球B的最大速率;
(2)小球B运动到圆弧曲面最高点时的速率;
(3)通过计算判断小球B能否与小球A再次发生碰撞.
▼优质解答
答案和解析
(1)A与B发生弹性碰撞,取水平向右为正方向,根据动量守恒定律和动能守恒得:
v0=
vA+MvB;
由动能守恒得:
•
v02=
•
vA2+
MvB2;
解得 vA=-2m/s,vB=4m/s
故B的最大速率为4m/s.
(2)B冲上C并运动到最高点时二者共速设为v,则
MvB=(M+2M)v
可以得到:v=
m/s.
(3)从B冲上C然后又滑下的过程,设BC分离时速度分别为vB′、vC′.
由水平动量守恒有
MvB=MvB′+2MvC′
机械能也守恒,有
MvB2=
MvB′2+
•2MvC′2
联立可以得到:vB′=-
m/s
由于|vB′|<|vA|,所有二者不会再次发生碰撞.
答:
(1)小球B的最大速率是4m/s;
(2)小球B运动到圆弧曲面最高点时的速率是
m/s.
(3)小球B不能与小球A再次发生碰撞.
| M |
| 2 |
| M |
| 2 |
由动能守恒得:
| 1 |
| 2 |
| M |
| 2 |
| 1 |
| 2 |
| M |
| 2 |
| 1 |
| 2 |
解得 vA=-2m/s,vB=4m/s
故B的最大速率为4m/s.
(2)B冲上C并运动到最高点时二者共速设为v,则
MvB=(M+2M)v
可以得到:v=
| 4 |
| 3 |
(3)从B冲上C然后又滑下的过程,设BC分离时速度分别为vB′、vC′.
由水平动量守恒有
MvB=MvB′+2MvC′
机械能也守恒,有
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
联立可以得到:vB′=-
| 4 |
| 3 |
由于|vB′|<|vA|,所有二者不会再次发生碰撞.
答:
(1)小球B的最大速率是4m/s;
(2)小球B运动到圆弧曲面最高点时的速率是
| 4 |
| 3 |
(3)小球B不能与小球A再次发生碰撞.
看了 如图所示,光滑水平面上有一质...的网友还看了以下:
在一幅比例尺是是1:30000的平面图上,量得AB两地相距12厘米,而要把AB画在1:50000的 2020-05-13 …
这是小红家的平面图,设计师是按1300的比例尺绘制的,请你帮小红完成下面各题.(1)量一量图中卧室 2020-07-27 …
我把问题打出来!我已量好半径了!大圆半径3厘米!小圆2厘米!是个环形!右图是用1:20的比例尺画的 2020-07-29 …
如何用PS将平面图形制作弯曲效果我想把一张平面图形弯曲后做出效果图,例如将一张长条图形高40*宽1 2020-07-30 …
英语翻译1.各立面图2.正面效果图3.平面布置图4.天花平面图,包括灯具布置图(标高为3000mm 2020-08-01 …
下面的小学校园平面图是长方形,请根据这个平面图完成以下各题.(1)量一量,算一算.(测量图上距离时 2020-08-01 …
读下面图文资料,回答问题.图l为黄河干流径流量和含沙量变化示意图,图2为黄河流域图.(1)黄河各河段 2020-11-17 …
在一幅比例尺为1:200的平面图上量得一间长方形教室的长是3cm,宽是2cm.1.求这间教室图上面积 2020-11-20 …
2.XX小学的一幢教学大楼,地基是长80米、宽30米的长方形,在平面图上量得它的宽是15厘米,平面图 2020-11-21 …
量量配制了一定浓度的盐水,他想利用这些盐水筛选出饱满的种子.为了测量出所配制出的盐水密度,他利用了托 2021-01-01 …