早教吧作业答案频道 -->数学-->
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.(1)证明:AC1⊥A1B;(2)设二面角A1-AB-C的正切值为15.求直线AA1与平面BCC1B1的距离.
题目详情
如图,三棱柱ABC-A1B1C1中,点A1在平面ABC内的射影D在AC上,∠ACB=90°,BC=1,AC=CC1=2.
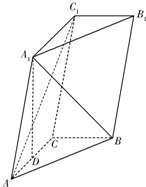
(1)证明:AC1⊥A1B;
(2)设二面角A1-AB-C的正切值为
.求直线AA1与平面BCC1B1的距离.

(1)证明:AC1⊥A1B;
(2)设二面角A1-AB-C的正切值为
| 15 |
▼优质解答
答案和解析
证明:(1)因为A1D⊥平面ABC,A1D⊂平面AA1C1C,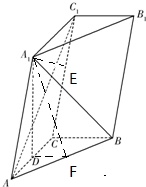
故平面AA1C1C⊥平面ABC,
又BC⊥AC,所以BC⊥平面AA1C1C,连接A1C.
因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1.
故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,
故∠A1FD为二面角A1-AB-C的平面角.
设AD=x则A1D=
,DF=
x,而tan∠A1FD=
=
,
故x=1,所以D是AC的中点,
故A1D=
为直线AA1与平面BCC1B1的距离.

故平面AA1C1C⊥平面ABC,
又BC⊥AC,所以BC⊥平面AA1C1C,连接A1C.
因为侧面AA1C1C为菱形,故AC1⊥A1C.
由三垂线定理得AC1⊥A1B.
(2)BC⊥平面AA1C1C,BC⊂平面BCC1B1.
故平面AA1C1C⊥平面BCC1B1.
作A1E⊥CC1,E为垂足,则A1E⊥平面BCC1B1.
作DF⊥AB,F为垂足,连接A1F.
由三垂线定理得A1F⊥AB,
故∠A1FD为二面角A1-AB-C的平面角.
设AD=x则A1D=
| 4-x2 |
| ||
| 5 |
| A1D |
| DF |
| 15 |
故x=1,所以D是AC的中点,
故A1D=
| 3 |
看了 如图,三棱柱ABC-A1B1...的网友还看了以下:
有关本初子午线的描述,正确的是()A.东西半球的分界线B.0°纬线C.东经和西经的界线D.在西半球 2020-04-24 …
下面说法正确的是()A.一个三角形内角度数的比是1:2:3,这是个锐角三角形B.国际儿童节和国庆节 2020-05-13 …
不能肯定两个平面一定垂直的情况是A.两个平面相交,所成二面角是直二面角B.一个平面经过另一个平面的 2020-05-13 …
初三二次函数某立交桥的桥拱为一段抛物线D'FD,在如图的平面直角坐标系中,顶点F的坐标为(0,8) 2020-05-16 …
若在一张白纸上从左至右依次画出一段红线,一段紫线,透过三棱镜观察这两条线,可能的视觉效果是A.红线 2020-06-02 …
下列正确的是()A”点动成线“中的线一定是直线B直线运动轨迹一定是平面或曲面C曲面上一定没有直线D 2020-06-15 …
1)已知平面内有4条直线a,b,c和d.直线a,b和c相交于一点.直线b,c和d也相交于一点,试确 2020-06-15 …
能够测量长度的是什么A线段B直线C射线D平行线 2020-06-26 …
在下列情况中,会造成触电事故的是A.站在干燥的木凳上的单手接触火线B.站在地上的人触到零线C.站在 2020-07-14 …
下列叙述正确的是()A.画直线AB=10厘米B.若AB=6,BC=2,那么AC=8或4C.河道改直可 2020-12-08 …