设O为锐角△ABC的外心，R为△ABC的外接圆半径，AO，BO，CO的延长线分别交BC，CA，AB于点D，E，F．求证：1AD+1BE+1CF=2R．

Question

设O为锐角△ABC的外心，R为△ABC的外接圆半径，AO，BO，CO的延长线分别交BC，CA，AB于点D，E，F．求证：(1)/(AD)+(1)/(BE)+(1)/(CF)=(2)/(R)．

Answer 1

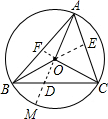证明：延长AD交 O于M，由于AD，BE，CF共点O，
∴(OD)/(AD)=(S△OBC)/(S△ABC)，(OE)/(BE)=(S△OAC)/(S△BAC)，(OF)/(CF)=(S△OAB)/(S△CAB)，
则(OD)/(AD)+(OE)/(BE)+(OF)/(CF)=1…①；
而(OD)/(AD)=(R-DM)/(2R-DM)=1-(R)/(2R-DM)=1-(R)/(AD)，
同理有，(OE)/(BE)=1-(R)/(BE)，(OF)/(CF)=1-(R)/(CF)，
代入①得：（1-(R)/(AD)）+（1-(R)/(BE)）+（1-(R)/(CF)）=1…②，
∴(R)/(AD)+(R)/(BE)+(R)/(CF)=2，
∴(1)/(AD)+(1)/(BE)+(1)/(CF)=(2)/(R)．