早教吧作业答案频道 -->数学-->
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.(1)判断命题“另一组邻边也相等的四边形为正方形”是真命题还是假命题?(2)如图
题目详情
对于一个四边形给出如下定义:有一组对角相等且有一组邻边相等,则称这个四边形为奇特四边形.
(1)判断命题“另一组邻边也相等的四边形为正方形”是真命题还是假命题?
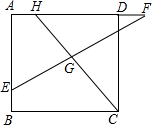
(2)如图,在正方形ABCD中,E为AB边上一点,F是AD延长线一点,BE=DF,连接EF,取EF的中点G,连接CG并延长交AD于点H,探究:四边形BCGE是否是奇特四边形,如果是,请证明你的结论;如果不是,请说明理由.
(3)在(2)的条件下,若四边形BCGE的面积是16,设BC=x,BE=y,
①求x+y的值;
②求当x+xy取最大值时FH的长.

(1)判断命题“另一组邻边也相等的四边形为正方形”是真命题还是假命题?
(2)如图,在正方形ABCD中,E为AB边上一点,F是AD延长线一点,BE=DF,连接EF,取EF的中点G,连接CG并延长交AD于点H,探究:四边形BCGE是否是奇特四边形,如果是,请证明你的结论;如果不是,请说明理由.
(3)在(2)的条件下,若四边形BCGE的面积是16,设BC=x,BE=y,
①求x+y的值;
②求当x+xy取最大值时FH的长.
▼优质解答
答案和解析
(1)假命题,如图,AB=AC,∠ABD=∠ACD,又DC=DB,明显四边形ABDC不是正方形.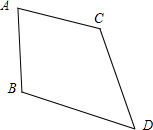
(2)连接CE,CF∵四边形ABCD是正方形,
∴BC=DC,∠EBC=∠FDC=90°,
在△EBC和△FDC中,
∴△CBE≌△CDF(SAS)
∴CE=CF,∠BCE=∠DCE
∴∠ECF=90°,
∵G是EF的中点,
∴GE=GC,∠EGC=90°,
∵GE=GC,∠EGC=∠B=90°
∴四边形BCGE是奇特四边形;
(3)①过点G作MN∥AB,GQ∥AD,
∴△GQE≌△GMC(AAS)
∴GQ=GM,
∴四边形BMGQ是正方形,S四边形BCGE=S正方形BMGQ,
∵四边形BCGE的面积是16,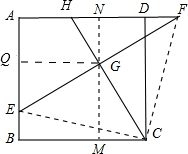
∴S正方形BMGQ=16
∴GQ=GM=AN=4,
∵G是EF的中点,
∴AN=FN=4,
∴AF=8
∵BE=DF,BC=AD,
∴BE+BC=AF=8
∵BC=x,BE=y
∴x+y=8;
②由①知y=8-x,
∴x+xy=x+x(8-x)=-x2+9x=-(x-
)2+
,
∴x+xy取最大值时,x=BC=4.5,y=BE=3.5
∴CE=CF=
=
,
∴FG=
∵Rt△FGH∽Rt△FNG
∴FG2=FN•FH
∵FN=4,FG=
,
∴FH=
.

(2)连接CE,CF∵四边形ABCD是正方形,
∴BC=DC,∠EBC=∠FDC=90°,
在△EBC和△FDC中,
|
∴△CBE≌△CDF(SAS)
∴CE=CF,∠BCE=∠DCE
∴∠ECF=90°,
∵G是EF的中点,
∴GE=GC,∠EGC=90°,
∵GE=GC,∠EGC=∠B=90°
∴四边形BCGE是奇特四边形;
(3)①过点G作MN∥AB,GQ∥AD,
∴△GQE≌△GMC(AAS)
∴GQ=GM,
∴四边形BMGQ是正方形,S四边形BCGE=S正方形BMGQ,
∵四边形BCGE的面积是16,

∴S正方形BMGQ=16
∴GQ=GM=AN=4,
∵G是EF的中点,
∴AN=FN=4,
∴AF=8
∵BE=DF,BC=AD,
∴BE+BC=AF=8
∵BC=x,BE=y
∴x+y=8;
②由①知y=8-x,
∴x+xy=x+x(8-x)=-x2+9x=-(x-
| 9 |
| 2 |
| 81 |
| 4 |
∴x+xy取最大值时,x=BC=4.5,y=BE=3.5
∴CE=CF=
(
|
| ||
| 2 |
∴FG=
| ||
| 4 |
∵Rt△FGH∽Rt△FNG
∴FG2=FN•FH
∵FN=4,FG=
| ||
| 4 |
∴FH=
| 65 |
| 16 |
看了 对于一个四边形给出如下定义:...的网友还看了以下:
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下 2020-05-13 …
已知平行六面体,与平面,交于两点。给出以下命题,其中真命题有(写出所有正确命题的序号)①点为线段的 2020-05-13 …
已知关于x的一元四次方程x4+px2+qx+r=0有三个相等的实根和另一个与之不同的实根,则下列三 2020-05-17 …
关于命题的一、有下列命题:1真命题都是定理2定理都是真命题3假命题不是命题4公理都是命题5命题都是 2020-07-04 …
填空题(只写答案)对于四边形ABCD,下面给出3个命题①若AB=BC,则CD=DA②若∠A=90° 2020-07-09 …
下列命题中:(1)锐角都相等;(2)大于直角且小于平角的角是钝角;(3)互为相反数的两个数的商是- 2020-07-14 …
已知四个命题:①若a<b,则-5+a>-5+b;②直角三角形只有一条高线;③对顶角相等;④三角形的 2020-07-15 …
下列命题中真命题有几个()①三角形的任意两边之和都大于第三边;②三角形的任意两角之和都大于第三个角 2020-07-29 …
下列命题中:①相等的角是对顶角;②同角的余角相等;③若|a|=|b|,则a=b;④内错角相等,其中 2020-07-29 …
3.下列说法中,错误的是()A.要说明一个命题为真,必须给出证明(过程).B.要说明一个命题为假, 2020-07-30 …