早教吧作业答案频道 -->数学-->
如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.(1)求证:四边形BFEP为菱形;(2)当点E在AD边上移动时,折痕的端点P、Q
题目详情
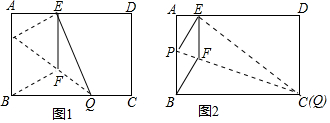
如图1,在矩形纸片ABCD中,AB=3cm,AD=5cm,折叠纸片使B点落在边AD上的E处,折痕为PQ,过点E作EF∥AB交PQ于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.
(1)求证:四边形BFEP为菱形;
(2)当点E在AD边上移动时,折痕的端点P、Q也随之移动;
①当点Q与点C重合时(如图2),求菱形BFEP的边长;
②若限定P、Q分别在边BA、BC上移动,求出点E在边AD上移动的最大距离.

▼优质解答
答案和解析
(1)证明:∵折叠纸片使B点落在边AD上的E处,折痕为PQ,
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EF∥AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形;
(2) ①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,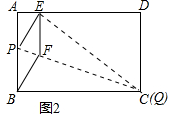
∴CE=BC=5cm,
在Rt△CDE中,DE=
=4cm,
∴AE=AD-DE=5cm-4cm=1cm;
在Rt△APE中,AE=1,AP=3-PB=3-PE,
∴EP2=12+(3-EP)2,
解得:EP=
cm,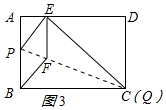
∴菱形BFEP的边长为
cm;
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm.
∴点B与点E关于PQ对称,
∴PB=PE,BF=EF,∠BPF=∠EPF,
又∵EF∥AB,
∴∠BPF=∠EFP,
∴∠EPF=∠EFP,
∴EP=EF,
∴BP=BF=EF=EP,
∴四边形BFEP为菱形;
(2) ①∵四边形ABCD是矩形,
∴BC=AD=5cm,CD=AB=3cm,∠A=∠D=90°,
∵点B与点E关于PQ对称,

∴CE=BC=5cm,
在Rt△CDE中,DE=
| CE2-CD2 |
∴AE=AD-DE=5cm-4cm=1cm;
在Rt△APE中,AE=1,AP=3-PB=3-PE,
∴EP2=12+(3-EP)2,
解得:EP=
| 5 |
| 3 |

∴菱形BFEP的边长为
| 5 |
| 3 |
②当点Q与点C重合时,如图2:
点E离点A最近,由①知,此时AE=1cm;
当点P与点A重合时,如图3所示:
点E离点A最远,此时四边形ABQE为正方形,AE=AB=3cm,
∴点E在边AD上移动的最大距离为2cm.
看了 如图1,在矩形纸片ABCD中...的网友还看了以下:
设计一个算法求以a为边长的等边三角形的外接圆的面积 2020-04-27 …
食物链中的数量变化关系以题为例b,c,d以a为食,e以d为食,f以e为食,g以b,c,f为食(图你 2020-05-23 …
帮我看看几道题↓如下(定有重谢)初2本人绝对诚信,1.在RT三角形中,角A为60度;c+b=21, 2020-06-06 …
一道MBA有关等比数列数学题po是以a为边长的正方形,p1是po的四边中点为顶点的正方形,p2是p 2020-07-04 …
1/lna=log以a为底e的对数?如果不是、那么对这个式子求导、y=log以a为底x的1/2次方 2020-08-01 …
关于几何图形的固定值比如说,正三角形的高为二分之根号三a(a为边长)正方形的对角线的一半为二分之根 2020-08-02 …
尺规作图,保留作图痕迹,不用写出作法,但要写出结论:(1)如图,已知线段a,请以a为边作一个等边三 2020-08-02 …
a的(log以a为底e的对数)次方=log以a为底的e对数 2020-11-06 …
x→0,求lim(a^x-1)/x结果是否为log以a为底e的对数 2020-12-09 …
如图为某反射弧的模式图(1)如图中A为,E为.(2)C为突触,其间进行传递的化学物质是,该物质使另一 2021-02-09 …