早教吧作业答案频道 -->数学-->
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.(1)求∠EAG的度数;(2)求证:HG∥CF;(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.
题目详情
如图,已知AB⊥CB,垂足为B,CG⊥BC,垂足为C,∠BAH=∠GCF=30°,AD平分∠BAF,AE平分∠BAG.
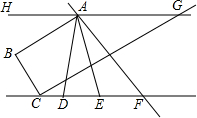
(1)求∠EAG的度数;
(2)求证:HG∥CF;
(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.

(1)求∠EAG的度数;
(2)求证:HG∥CF;
(3)试判断∠DAE与∠AFC之间的数量关系,并说明理由.
▼优质解答
答案和解析
(1)∵∠BAH=30°,
∴∠BAG=180°-30°=150°,
∵AE平分∠BAG,
∴∠EAG=
∠BAG=75°;
(2)∵AB⊥CB,垂足为B,CG⊥BC,垂足为C,
∴AB∥CG,
∴∠AGC=∠HAB=30°,
∵∠BAH=∠GCF=30°,
∴∠AGC=∠GCF,
∴HG∥CF;
(3)∠AFC=2∠DAE,
理由:设∠DAE=x,∠EAF=y,
∵AD平分∠BAF,AE平分∠BAG,
∴∠BAE=∠GAE,∠BAD=∠FAD=x+y,
∴x+y+x=y+∠GAF,
∴∠GAF=2x=2∠DAE,
∵HG∥CF,
∴∠AFC=∠GAF,
∴∠AFC=2∠DAE.
∴∠BAG=180°-30°=150°,
∵AE平分∠BAG,
∴∠EAG=
| 1 |
| 2 |
(2)∵AB⊥CB,垂足为B,CG⊥BC,垂足为C,
∴AB∥CG,
∴∠AGC=∠HAB=30°,
∵∠BAH=∠GCF=30°,
∴∠AGC=∠GCF,
∴HG∥CF;
(3)∠AFC=2∠DAE,
理由:设∠DAE=x,∠EAF=y,
∵AD平分∠BAF,AE平分∠BAG,
∴∠BAE=∠GAE,∠BAD=∠FAD=x+y,
∴x+y+x=y+∠GAF,
∴∠GAF=2x=2∠DAE,
∵HG∥CF,
∴∠AFC=∠GAF,
∴∠AFC=2∠DAE.
看了 如图,已知AB⊥CB,垂足为...的网友还看了以下:
函数是研究()A常量之间的对应关系的.B常量与变量之间的对应关系的C变量于常量之间的对应关系的D常 2020-04-26 …
在△ABC内任取一点P(如图①),连接PB、PC,探索∠BPC与∠A,∠ABP,∠ACP之间的数量 2020-07-20 …
若乘积的两个因数是a,b,请写出ab,a+b与a-b之间的等量关系式若乘积的两个因数是a,b,(a 2020-07-21 …
如图表示不同遮光处理对铁线莲光合作用的影响,其中叶绿素a/b表示叶绿素a含量与叶绿素b含量之比.净 2020-07-22 …
度量空间的并集是不是还是度量空间当然,有限并和无限并,能否举例? 2020-07-30 …
下列说法中正确的是()A.立定跳远中,运动员的成绩依据为运动员的位移大小B.有大小、有方向的量是矢量 2020-10-30 …
已知向量a=(cos3x/2,sin3x/2),b=(cosx/2,-sinx/2),且x属于[0. 2020-11-02 …
(2014•临沂二模)一颗质量为m的子弹以v0的速度水平射入置于光滑水平面上的质量为M的木块A并留在 2020-11-13 …
试探索GE,CE,BG之间的数量关系,并说明你的结论,注意:问题是3条线试探索GE,CE,BG之间的 2020-11-28 …
画3个形状、大小不同的等腰三角形ABC,其中AB=AC,BD为边AC上的高.⑴用量角器分别量出∠CB 2020-12-07 …