早教吧作业答案频道 -->数学-->
如图,CD是Rt△ABC斜边上的高,点G是DC的延长线上一点,作AF⊥BG交CD于点E.垂足是点F.①求证:CD2=ED•DG;②如果将此题目中的条件“DC的延长线”改为“CD的延长线”,其它条件不变,那么
题目详情
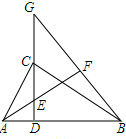
如图,CD是Rt△ABC斜边上的高,点G是DC的延长线上一点,作AF⊥BG交CD于点E.垂足是点F.
①求证:CD2=ED•DG;
②如果将此题目中的条件“DC的延长线”改为“CD的延长线”,其它条件不变,那么①中的结论是否仍然成立?为什么?
①求证:CD2=ED•DG;
②如果将此题目中的条件“DC的延长线”改为“CD的延长线”,其它条件不变,那么①中的结论是否仍然成立?为什么?

▼优质解答
答案和解析
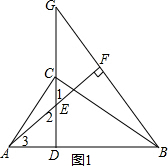 证明:①∵∠ACB=90°,CD⊥AB,
证明:①∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCD,
∴Rt△ACD∽Rt△CBD,
∴
=
,
∴CD2=AD•BD,
又∵AF⊥BG,GD⊥AB,
∴∠EDA=∠EFG=∠GDB=90°,
∵∠1=∠2,
∴∠G=∠3,
∴△BGD∽△ADE,
∴
=
,
∴AD•BD=DG•DE
∴CD2=DE•DG;
②①中的结论仍然成立,
理由:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCD,
∴Rt△ACD∽Rt△CBD,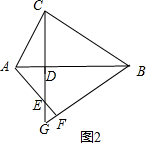
∴
=
,
∴CD2=AD•BD,
又∵AF⊥BG,GD⊥AB,
∴∠EDA=∠EFG=∠GDB=90°,
∵∠1=∠2,
∴∠G=∠3,
∴△BGD∽△ADE,
∴
=
,
∴AD•BD=DG•DE
∴CD2=DE•DG.
 证明:①∵∠ACB=90°,CD⊥AB,
证明:①∵∠ACB=90°,CD⊥AB,∴∠ACD+∠BCD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCD,
∴Rt△ACD∽Rt△CBD,
∴
| CD |
| BD |
| AD |
| CD |
∴CD2=AD•BD,
又∵AF⊥BG,GD⊥AB,
∴∠EDA=∠EFG=∠GDB=90°,
∵∠1=∠2,
∴∠G=∠3,
∴△BGD∽△ADE,
∴
| GD |
| AD |
| BD |
| DE |
∴AD•BD=DG•DE
∴CD2=DE•DG;
②①中的结论仍然成立,
理由:∵∠ACB=90°,CD⊥AB,
∴∠ACD+∠BCD=90°,∠ACD+∠CAD=90°,
∴∠CAD=∠BCD,
∴Rt△ACD∽Rt△CBD,

∴
| CD |
| BD |
| AD |
| CD |
∴CD2=AD•BD,
又∵AF⊥BG,GD⊥AB,
∴∠EDA=∠EFG=∠GDB=90°,
∵∠1=∠2,
∴∠G=∠3,
∴△BGD∽△ADE,
∴
| GD |
| AD |
| BD |
| DE |
∴AD•BD=DG•DE
∴CD2=DE•DG.
看了 如图,CD是Rt△ABC斜边...的网友还看了以下:
读图,回答下列问题:(1)写出A、B、D点所在的半球(东西半球与南北半球):A,;B,;D,.(2 2020-05-13 …
权利要求书撰写与保护范围的认定一个设计,特征有:A,B,C,D,E其中,A,B,C是重要设计点,一 2020-05-17 …
A,B,C,D,E五位同学进入了乒乓球决赛,猜一下他们的名次.A说:“B是第三名,C是第五。”B说 2020-06-06 …
a→b→c→d是一条捕食食物链,下面有关这条食物链的叙述错误的是()A.c与b间是捕食芙系B.物质 2020-06-21 …
如图所示的是一种按钮开关的构造截面图,其中()A.B是导体,C、D是绝缘体B.C是导体,D是绝缘体 2020-06-29 …
关于皮带传动中,A是主动轮,B,C和D是从动轮.其中A带动B,B和C是同轴不同直径的轮,C带动D转 2020-07-01 …
sumif嵌套or或者and比方A列中是一堆字母,或A或B或C或D,数目各不同,B列是对应的数字要 2020-07-23 …
a,b,c,d都是不同的质数.甲数=a*b*c,乙数=a*b*c*d,则().a.甲是乙的倍数b. 2020-07-31 …
填空1.设A、B是集合,|A|=6,|B|=4,则共可定义个从A到B的映射.2.若是与间的一一映射 2020-08-01 …
(1)A为直线a外一点,B是直线a上一点,点A到直线a的距离为3厘米,则线段AB的长度的取值范围是 2020-08-01 …