早教吧作业答案频道 -->数学-->
过点P(1,0)的直线l与曲线C:+y2=1交于A、B两点过点P还有一直线l′与曲线C交于C、D两点(与A、B不重合)若A、C、B、D四点共圆试求l与l′的倾斜角之间应满足什么条件?并说明理由.
题目详情
过点P(1,0)的直线l与曲线C: 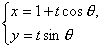 +y 2 =1交于A、B两点 过点P还有一直线l′与曲线C交于C、D两点(与A、B不重合) 若A、C、B、D四点共圆 试求l与l′的倾斜角之间应满足什么条件?并说明理由.
+y 2 =1交于A、B两点 过点P还有一直线l′与曲线C交于C、D两点(与A、B不重合) 若A、C、B、D四点共圆 试求l与l′的倾斜角之间应满足什么条件?并说明理由.
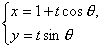 +y 2 =1交于A、B两点 过点P还有一直线l′与曲线C交于C、D两点(与A、B不重合) 若A、C、B、D四点共圆 试求l与l′的倾斜角之间应满足什么条件?并说明理由.
+y 2 =1交于A、B两点 过点P还有一直线l′与曲线C交于C、D两点(与A、B不重合) 若A、C、B、D四点共圆 试求l与l′的倾斜角之间应满足什么条件?并说明理由.
▼优质解答
答案和解析
解析:
应满足倾斜角互补.由题设可知l′:(t为参数),θ∈[0 π),则(1+t cosθ)2+2t2 sin2θ-2=0,即(1+sin2θ)t2+2t cosθ-1=0.∴|PD|·|PC|=|t1 ·t2|=.而|PA|·|PB|=|t1·t2|= ∵A、C、B、D四点共圆 ∴|PA|·|PB|=|PC|·|PD| 即=.∴sin2α=sin2θ.∴sinα=sinθ.∵A、B、C、D不重合 故α+θ=π 即两直线倾斜角互补.
解析:
应满足倾斜角互补.由题设可知l′:(t为参数),θ∈[0 π),则(1+t cosθ)2+2t2 sin2θ-2=0,即(1+sin2θ)t2+2t cosθ-1=0.∴|PD|·|PC|=|t1 ·t2|=.而|PA|·|PB|=|t1·t2|= ∵A、C、B、D四点共圆 ∴|PA|·|PB|=|PC|·|PD| 即=.∴sin2α=sin2θ.∴sinα=sinθ.∵A、B、C、D不重合 故α+θ=π 即两直线倾斜角互补.
看了 过点P(1,0)的直线l与曲...的网友还看了以下:
数学14455555圆A:(x+2)^2+y^2=1与点A(-2,0),B(2,0),分别说明满足 2020-05-12 …
已知焦距为4的椭圆C:x^2/a^2+y^2/b^2=1(a>b>0),F2为椭圆C的右焦点,AB 2020-05-15 …
已知椭圆C:x2a2+y2=1(a>1)的右焦点为F(c,0)(c>1),点P在圆O:x2+y2= 2020-06-21 …
已知椭圆(x*2/a*2)+(y*2/b*2)=1(a>b>0)的两个焦点分别为F1(-1,0)F 2020-06-21 …
在学习《5.1圆》这一节时,小明遇到了一个问题:如图(1),△ABC与△DBC中,∠A=∠D=90 2020-07-11 …
椭圆x2a2+y2b2=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,直线l过F2交椭 2020-07-30 …
已知圆A:(x+2)^2+y^2=25/4,圆B:(x-2)^2+y^2=0.25,动圆p与圆A, 2020-07-31 …
如图,已知圆G:(x-2)^2+y^2=r^2是椭圆x^2/16+y^2=1的内接△ABC的内切圆 2020-07-31 …
1.圆A的直径是圆B直径的5分之3,圆B的周长是圆A的()倍,圆B的面积是圆A的(1.圆A的直径是 2020-08-01 …
圆A与圆B的直径比是2:1,圆A的面积比圆B多18.84平方米,圆A的面积是多少 2020-12-14 …