早教吧作业答案频道 -->数学-->
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,AM=λAF(λ∈R,λ>0).(Ⅰ)设ND中点为Q,λ=12,求证:MQ
题目详情
如图,在棱台ABC-FED中,△DEF与△ABC分别是棱长为1与2的正三角形,平面ABC⊥平面BCDE,四边形BCDE为直角梯形,BC⊥CD,CD=1,N为AB中点,
=λ
(λ∈R,λ>0).
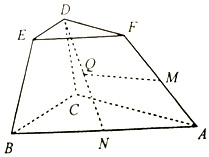
(Ⅰ)设ND中点为Q,λ=
,求证:MQ∥平面ABC;
(Ⅱ)若M到平面BCD的距离为
,求直线MC与平面BCD所成角的正弦值.
| AM |
| AF |

(Ⅰ)设ND中点为Q,λ=
| 1 |
| 2 |
(Ⅱ)若M到平面BCD的距离为
3
| ||
| 4 |
▼优质解答
答案和解析
(Ⅰ)证明:延长三棱台的三条侧棱,设交点为S,当λ=
时M为FA的中点,
设CD中点为R,连MR,MQ,RQ,
在梯形ACDF中,中位线MR∥AC,又MR⊄平面ABC,AC⊂平面ABC,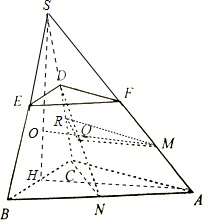
∴MR∥平面ABC;
在△CDN中,中位线QR∥CN,又QR⊄平面ABC,CN⊂平面ABC,
∴QR∥平面ABC,
又MR∩QR=R且MR⊂平面MQR,QR⊂平面MQR,
∴平面MQR∥平面ABC,
又MQ⊂平面MQR
∴MQ∥平面ABC;
(Ⅱ) 设AB中点为H,连SH,AH,在△SAH中,作MO∥AH且交SH于点O,
∵平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,
AH⊂平面ABC,AH⊥BC,∴AH⊥平面SBC,
又MO∥AH,∴MO⊥平面SBC(D),
∴MO为M到平面SBC的距离,MO=
.
且∠MCO为直线MC与平面BCD所成角.
∵平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,
CD⊂平面BCDE,CD⊥BC,∴CD⊥平面ABC,
又AC⊂平面ABC,∴CD⊥AC,
在Rt△SAC中,DF∥AC,DF=1,AC=2,CD=1,
由
=
=
,得
=
,即M为FA的中点.
∴CF⊥SA,又CF=
,FM=
,∴CM=
.
在Rt△MCO中,sin∠MCO=
=
.
故直线MC与平面BCD所成角的正弦值为
| 1 |
| 2 |
设CD中点为R,连MR,MQ,RQ,
在梯形ACDF中,中位线MR∥AC,又MR⊄平面ABC,AC⊂平面ABC,

∴MR∥平面ABC;
在△CDN中,中位线QR∥CN,又QR⊄平面ABC,CN⊂平面ABC,
∴QR∥平面ABC,
又MR∩QR=R且MR⊂平面MQR,QR⊂平面MQR,
∴平面MQR∥平面ABC,
又MQ⊂平面MQR
∴MQ∥平面ABC;
(Ⅱ) 设AB中点为H,连SH,AH,在△SAH中,作MO∥AH且交SH于点O,
∵平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,
AH⊂平面ABC,AH⊥BC,∴AH⊥平面SBC,
又MO∥AH,∴MO⊥平面SBC(D),
∴MO为M到平面SBC的距离,MO=
3
| ||
| 4 |
且∠MCO为直线MC与平面BCD所成角.
∵平面ABC⊥平面BCDE,平面ABC∩平面BCDE=BC,
CD⊂平面BCDE,CD⊥BC,∴CD⊥平面ABC,
又AC⊂平面ABC,∴CD⊥AC,
在Rt△SAC中,DF∥AC,DF=1,AC=2,CD=1,
由
| MO |
| AH |
| ||||
|
| 3 |
| 4 |
| SM |
| SA |
| 3 |
| 4 |
∴CF⊥SA,又CF=
| 2 |
| ||
| 2 |
| ||
| 2 |
在Rt△MCO中,sin∠MCO=
| MO |
| MC |
3
| ||
| 20 |
故直线MC与平面BCD所成角的正弦值为
3
|
看了 如图,在棱台ABC-FED中...的网友还看了以下:
写出下列各组离子之间发生双水解的离子方程式.1.Fe3+与CO32-2.Al3+与C写出下列各组离 2020-04-11 …
(1)过点P(-3,1)且与直线2x+y-3=0平行的直线的方程;(1)过点P(-3,1)且与直线 2020-06-06 …
英语翻译2.3.1.4货物码放符合规定距离.2.3.1.4.1垛与垛间距不少于20厘米.2.3.1 2020-07-10 …
比较下列各组三角函数值的大小1,cos250°与cos255°2.cos5π/9与cos7π/比较 2020-07-19 …
如图,直线y=1/2x与y=k/x(k>o,x>o)交于点a,将直线y=1/2x向上平移4个单位后 2020-07-20 …
n为非0自然数,试证n^13n定能被2730整除.2730=2*3*5*7*13,n^13-n=n 2020-07-22 …
有关数列下列说法正确的是①数列1,2,3与数列3,2,1是同一数列.②数列1,2,3与数列1,2, 2020-07-23 …
下面式子中,是同类项的A.2a和aB.4b和4aC.100和1/2D.6x(^2)y和6y(^2) 2020-08-01 …
已知K=1.4×10-5,K=1.8×10-10,K=1.1×10-10,将等体积的0.0020mo 2021-01-09 …
我们知道“2分之1乘与3分之2等于3分之1,2分之1乘与3分之2乘与4分之3等于4分之1,2分之1乘 2021-01-11 …
 扫描下载二维码
扫描下载二维码
