早教吧作业答案频道 -->数学-->
把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2(1)
题目详情
把几个图形拼成一个新的图形,再通过两种不同的方法计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的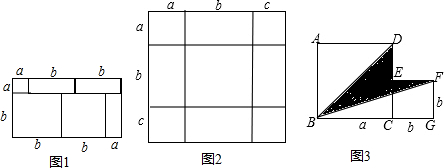 问题:
问题:
已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
例如,由1,可得等式:(a+2b)(a+b)=a2+3ab+2b2
(1)如图2,将几个面积不等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的形式表示这个大正方形的面积,你能发现什么结论?请用等式表示出来.
(2)利用(1)中所得到的结论,解决下面的
 问题:
问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)如图3,将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连接BD和BF.若这两个正方形的边长满足a+b=10,ab=20,请求出阴影部分的面积.
▼优质解答
答案和解析
(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2 =(a+b+c)2-2(ab+ac+bc)=121-76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2-
(a+b)•b-
a2=
a2+
b2-
ab=
(a+b)2-
ab=
×102-
×20=50-30=20.
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2 =(a+b+c)2-2(ab+ac+bc)=121-76=45;
(3)∵a+b=10,ab=20,
∴S阴影=a2+b2-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
看了 把几个图形拼成一个新的图形,...的网友还看了以下:
有一个算术题,9以下的数字和别的什么算起来最后可以等于520.怎么算?我以前在杂志上看到过,一个算 2020-04-07 …
一道算术题(12X21X4.5X10.2)÷(15X4X0.7X5.1)这道算术题要用简算来算,可 2020-05-13 …
打开网络搜索,有人发现关于算命的主题可以找到172个网站和12000多个网页。其中算命的方式很多, 2020-05-17 …
把1到25排列5行横竖斜都等于75谁会属于是智力问题.294753618根据9宫继续往下算我以算出 2020-06-11 …
关于约等于 一道题中已经有一个结果是约等于的时候 再用这个结果进行其他简单的运算(简单运算即不约等 2020-06-27 …
7500除以25乘30递等式可以巧算吗,可以的话,列式给我,再计算出来;不可以的话,再列式,算出来 2020-07-18 …
计算等腰梯形面积已知等腰梯形四边长,不可以计算出高,怎么计算出面积.这是为了计算的方便.不可以计算 2020-08-02 …
算术好等于数学好么?心算能力强的孩子是神童吗?一般孩子可以练出《最强大脑》5岁小选手葛韵霖的心算能力 2020-10-30 …
单位也是可以计算的这句话对么?比如求面积单位,CM×CM等于CM的平方表示面积等.那么其他所有单位在 2020-11-28 …
单位也是可以计算的,这句话对么?比如求面积单位,CM×CM等于CM的平方表示面积,等等..那么其他所 2020-11-28 …