早教吧作业答案频道 -->数学-->
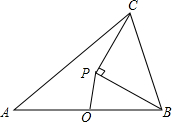
如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是.
题目详情
如图,已知线段AB=4,O为AB的中点,P是平面内的-个动点,在运动过程中保持OP=1不变,连结BP,将PB绕点P逆时针旋转90°到PC,连结BC、AC,则线段AC长的取值范围是___.

▼优质解答
答案和解析
如图所示:过点C作CD⊥y轴,垂足为D,过点P作PE⊥DC,垂足为E,延长EP交x轴于点F.
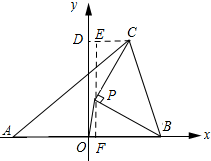
∵AB=4,O为AB的中点,
∴A(-2,0),B(2,0).
设点P的坐标为(x,y),则x2+y2=1.
∵∠EPC+∠BPF=90°,∠EPC+∠ECP=90°,
∴∠ECP=∠FPB.
由旋转的性质可知:PC=PB.
在△ECP和△FPB中
,
∴△ECP≌△FPB.
∴EC=PF=y,FB=EP=2-x.
∴C(x+y,y+2-x).
∵AB=4,O为AB的中点,
∴AC=
=
.
∵x2+y2=1,
∴AC=
.
∵-1≤y≤1,
∴
≤AC≤3
.
故答案为:
≤AC≤3
.

∵AB=4,O为AB的中点,
∴A(-2,0),B(2,0).
设点P的坐标为(x,y),则x2+y2=1.
∵∠EPC+∠BPF=90°,∠EPC+∠ECP=90°,
∴∠ECP=∠FPB.
由旋转的性质可知:PC=PB.
在△ECP和△FPB中
|
∴△ECP≌△FPB.
∴EC=PF=y,FB=EP=2-x.
∴C(x+y,y+2-x).
∵AB=4,O为AB的中点,
∴AC=
| (x+y+2)2+(y+2-x)2 |
| 2x2+2y2+8y+8 |
∵x2+y2=1,
∴AC=
| 10-8y |
∵-1≤y≤1,
∴
| 2 |
| 2 |
故答案为:
| 2 |
| 2 |
看了 如图,已知线段AB=4,O为...的网友还看了以下:
已知:实数a,b,c在数轴上的位置如图所示,且,a的绝对值=b的绝对值.化简:a的绝对值+a和b的 2020-04-05 …
已知实数a,b,c在数轴上的位置如图所示,且绝对值a=绝对值b化简绝对值a加绝对值a加b-根号c- 2020-04-06 …
如果A分之C>0,B分之C>0,那么B分之A()0填>,<,=若Y分之XZ<0,YZ>0,那么X( 2020-04-25 …
若三点A(2,2)B(a,0)C(0,b)(ab不=0)共线,则(1/a)+(1/b)的值等于( 2020-05-16 …
已知二次函数的图像,求结论,已知二次函数y=ax²+bx+c(a≠0)的图像,下列四个结论①b<0 2020-07-19 …
=SUMIF(BM!$C$2:OFFSET(BM!$C$2,0,$B$2-1),OFFSET(BM 2020-07-23 …
下列二次根式中,属于同类二次根式的是A.√ab3c5和-3√c2/ab(a<0,b<0,c>0)B 2020-07-30 …
已知a,b,c满足c<b<a且ac<0,则下列不等式中恒成立的是(填序号)①b/a>c/a②(b- 2020-08-01 …
程序片断如下:if(a.equals(“0”)&&b.equals(“0”)){e=1},在测试时有 2020-11-01 …
抛物线与x轴交于a.b两点.其解析式为y=ax2+bx+c.与y轴交于点c.角obc=45度抛物线开 2021-01-10 …